
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способы расчета электрических полей. Принцип суперпозиции
|
|
|
|
Лекция 2.2
Поле точечного заряда.
Из формулы закона Кулона (2.1.1) и определения напряженности (2.1.2) следует, что напряженность поля, созданного точечным зарядом q в точке на расстоянии r от него рассчитывается по формуле
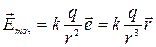 , (2.2.1)
, (2.2.1)
где  - орт, направленный от заряда – источника поля к точке, в которой ищется напряженность,
- орт, направленный от заряда – источника поля к точке, в которой ищется напряженность,  - радиус-вектор, проведенный от заряда к точке, в которой рассчитываем напряженность электрического поля. Таким образом, напряженность поля в любой точке направлена вдоль прямой, соединяющей ее с зарядом и эти же линии являются силовыми (рис. 2.4).
- радиус-вектор, проведенный от заряда к точке, в которой рассчитываем напряженность электрического поля. Таким образом, напряженность поля в любой точке направлена вдоль прямой, соединяющей ее с зарядом и эти же линии являются силовыми (рис. 2.4).
Из формулы потенциальной энергии взаимодействия двух точечных зарядов (2.1.3) и определения потенциала (2.1.4) получим выражение для потенциала поля точечного заряда
 . (2.2.2)
. (2.2.2)
 Напомним, что потенциал (как и потенциальная энергия) может быть определен только с точностью до произвольной постоянной. При определении потенциала точечного заряда обычно полагают, что при бесконечном удалении от заряда потенциал равен нулю. При этом условии const = 0 и потенциал точечного заряда находится по формуле
Напомним, что потенциал (как и потенциальная энергия) может быть определен только с точностью до произвольной постоянной. При определении потенциала точечного заряда обычно полагают, что при бесконечном удалении от заряда потенциал равен нулю. При этом условии const = 0 и потенциал точечного заряда находится по формуле
 (2.2.3)
(2.2.3)
Таким образом, во всех точках равноотстоящих от заряда потенциал одинаков, т.е. эквипотенциальными поверхностями являются сферы (рис. 2.2.1).
Способы расчета электрических полей.
Существует два способа расчета напряженности электрического поля:
1 принцип суперпозиции,
2 теорема Гаусса.
Потенциал можно найти также двумя способами либо по принципу суперпозиции, либо через связь с напряженностью (2.1.11).
Принцип суперпозиции.
Если электрическое поле создается несколькими точечными зарядами, то электрические поля каждого заряда в отдельности накладываются друг на друга. Результат наложения полей и будет так называемым результирующим полем. В этом заключается принцип суперпозиции.
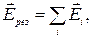
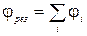 , (2.2.4)
, (2.2.4)
где 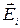 и
и 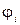 - соответственно напряженность и потенциал поля, созданного одним точечным зарядом.
- соответственно напряженность и потенциал поля, созданного одним точечным зарядом.
Если же поле создается некоторым заряженным телом, то это тело нужно разбить на бесконечно малые элементы, которые можно полагать точечными зарядами, а затем воспользоваться принципом суперпозиции
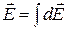 ,
, 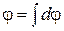 . (2.2.5)
. (2.2.5)
Рассмотрим примеры.
1. Пусть поле создается двумя точечными зарядами находящимися в вершинах равностороннего треугольника. Сторона треугольника равна 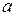 . Найдем величину вектора напряженности результирующего поля в третьей вершине (см. рис.2.2.2). Согласно принципу суперпозиции запишем
. Найдем величину вектора напряженности результирующего поля в третьей вершине (см. рис.2.2.2). Согласно принципу суперпозиции запишем 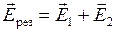 . Возведем в квадрат полученное выражение
. Возведем в квадрат полученное выражение 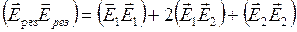 . Угол между векторами
. Угол между векторами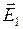 и
и 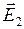 равен
равен  . Раскроем скалярные произведения
. Раскроем скалярные произведения  . Модуль вектора
. Модуль вектора  равен
равен 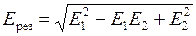 . Со
. Со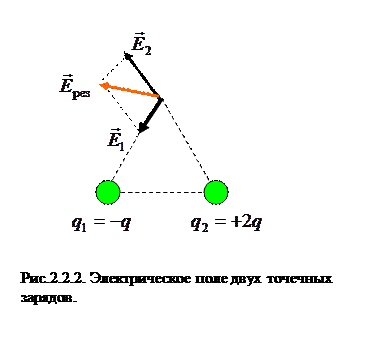 гласно (2.2.4) и (2.2.1) можно записать
гласно (2.2.4) и (2.2.1) можно записать 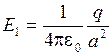 ,
,  . После несложных преобразований приходим к ответу
. После несложных преобразований приходим к ответу 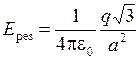 . Направление вектора
. Направление вектора  находится по правилу сложения векторов.
находится по правилу сложения векторов.
Если модули зарядов q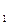 и q
и q одинаковы, система называется электрическим диполем. Электрический диполь– это система из двух одинаковых по модулю разноименных точечных зарядов
одинаковы, система называется электрическим диполем. Электрический диполь– это система из двух одинаковых по модулю разноименных точечных зарядов 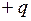 и
и  , находящихся на некотором расстоянии
, находящихся на некотором расстоянии  друг от друга. Когда говорят о поле диполя, то предполагают сам диполь точечным, то есть считают расстояние
друг от друга. Когда говорят о поле диполя, то предполагают сам диполь точечным, то есть считают расстояние 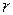 от диполя до интересующей нас точки поля значительно больше
от диполя до интересующей нас точки поля значительно больше  .
.
Поле диполя обладает осевой симметрией, поэтому картина поля в любой плоскости, проходящей через ось диполя, одна и та же и вектор 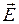 лежит в этой плоскости.
лежит в этой плоскости.
Найдем потенциал поля диполя (см. рис. 2.2.3).
 Согласно принципу суперпозиции потенциал системы точечных зарядов в заданной точке равен
Согласно принципу суперпозиции потенциал системы точечных зарядов в заданной точке равен

 .
.
Так как  , то
, то  и
и 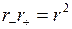 . С учетом этого
. С учетом этого
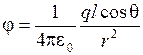
| (2.2.6) |
Потенциал поля диполя убывает с расстоянием быстрее, чем потенциал точечного заряда (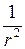 вместо
вместо 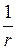 ).
).
Введем понятие дипольного момента. Для этого обозначим  - плечо диполя – вектор, направленный от отрицательного заряда к положительному. Тогда
- плечо диполя – вектор, направленный от отрицательного заряда к положительному. Тогда
электрический дипольный момент – вектор, равный произведению модуля заряда на плечо
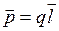 . .
| (2.2.7) |
С учетом (2.2.7) перепишем формулу (2.2.6) следующим образом
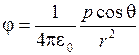 . .
| (2.2.8) |
С помощью формулы (2.1.11) вычислим проекции  и
и 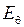 .
.
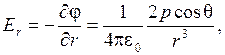  . .
|
Отсюда модуль вектора 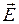 равен
равен
 . .
| (2.2.9) |
В частности, при угле 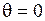 , мы получаем выражение для поля вдоль оси диполя
, мы получаем выражение для поля вдоль оси диполя 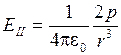 . При угле
. При угле 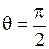 , мы получаем выражение для поля перпендикулярно оси
, мы получаем выражение для поля перпендикулярно оси 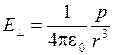 . При одном и том же
. При одном и том же 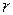 напряженность
напряженность 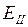 в два раза больше
в два раза больше  .
.
А теперь поместим диполь во внешнее электрическое поле. Рассчитаем силу, действующую на диполь, и его энергию в поле. Пусть 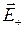 и
и  - напряженности внешнего поля в точках, где расположены положительный и отрицательный заряды диполя. Тогда результирующая сила, действующая на диполь, равна
- напряженности внешнего поля в точках, где расположены положительный и отрицательный заряды диполя. Тогда результирующая сила, действующая на диполь, равна
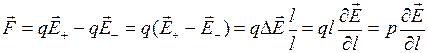 . .
|
Здесь 
 - это приращение вектора
- это приращение вектора 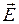 на отрезке, равном длине диполя
на отрезке, равном длине диполя  , в направлении вектора
, в направлении вектора  .
.
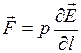 . (2.2.10) (2.2.10) . (2.2.10) (2.2.10)
|
 Из формулы видно, что сила, приложенная к диполю в однородном поле равна нулю (т.к.
Из формулы видно, что сила, приложенная к диполю в однородном поле равна нулю (т.к.  ), в неоднородном электрическом поле ─ направлена в сторону усиления поля. Кроме того, на диполь будет действовать момент сил
), в неоднородном электрическом поле ─ направлена в сторону усиления поля. Кроме того, на диполь будет действовать момент сил  , под действием которого диполь будет разворачиваться дипольным моментом вдоль напряженности внешнего поля.
, под действием которого диполь будет разворачиваться дипольным моментом вдоль напряженности внешнего поля.
 ; ;  . (2.2.11) . (2.2.11)
|
Энергия диполя в поле равна  . Здесь
. Здесь 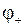 и
и 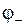 потенциалы поля в точке нахождения положительного и отрицательного зарядов диполя соответственно. Поскольку
потенциалы поля в точке нахождения положительного и отрицательного зарядов диполя соответственно. Поскольку  выражение для энергии диполя примет вид
выражение для энергии диполя примет вид
 (2.2.12) (2.2.12)
|
Из формулы следует, что минимальную энергию диполь имеет при 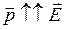 (положение устойчивого равновесия). При отклонении от этого положения, возникает момент сил, стремящихся вернуть диполь в это положение.
(положение устойчивого равновесия). При отклонении от этого положения, возникает момент сил, стремящихся вернуть диполь в это положение.
2. Разберем второй случай, когда заряд распределен непрерывно.
Найдем напряженность электрического поля тонкого равномерно заряженного с линейной плотностью  стержня на оси, проходящей через его середину и перпендикулярной стержню (см. рис. 2.8). Длина стержня равна
стержня на оси, проходящей через его середину и перпендикулярной стержню (см. рис. 2.8). Длина стержня равна 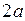 .
.
 Мысленно можно разбить стержень на заряженные малые отрезки, которые можно считать точечными зарядами (
Мысленно можно разбить стержень на заряженные малые отрезки, которые можно считать точечными зарядами (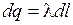 ). Напряженность поля такого заряда равна
). Напряженность поля такого заряда равна 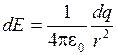 . Согласно принципу суперпозиции
. Согласно принципу суперпозиции 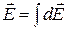 . Из рис.2.2.5 видно, что результирующее поле будет направлено строго по оси
. Из рис.2.2.5 видно, что результирующее поле будет направлено строго по оси 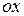 . Поэтому для отыскания модуля
. Поэтому для отыскания модуля  следует суммировать только проекции
следует суммировать только проекции 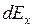 .
.

|
Прежде чем перейти к интегралу, преобразуем полученное выражение. Переменные величины 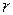 ,
,  и
и  свяжем через тангенс угла
свяжем через тангенс угла  :
:
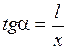 . .
|
Поскольку для всех 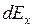 значение
значение  одинаковое, то эту величину можем считать постоянной. Продифференцируем это выражение:
одинаковое, то эту величину можем считать постоянной. Продифференцируем это выражение:
 . .
|
Выразим все переменные через угол  .
.
  . .
|
Подставим полученные замены в выражение для 
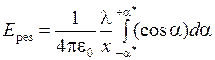 . .
|
Пределы интегрирования 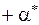 и
и 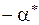 соответствуют угловым размерам стержня относительно оси
соответствуют угловым размерам стержня относительно оси 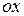 для данного значения
для данного значения  . Результат интегрирования:
. Результат интегрирования: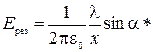 . Учтем, что
. Учтем, что  и получим окончательное выражение
и получим окончательное выражение
 . (2.2.13)
. (2.2.13)
Если стержень будет очень длинным (бесконечным), т.е. x «a, из (2.2.13) следует
 (2.2.14)
Определим в этом последнем случае также потенциал поля. Для этого
воспользуемся связью между напряженностью и потенциалом. Как видно из
(2.2.14) в случае бесконечного стержня напряженность в любой точке поля
имеет только радиальную составляющую Е (2.2.14)
Определим в этом последнем случае также потенциал поля. Для этого
воспользуемся связью между напряженностью и потенциалом. Как видно из
(2.2.14) в случае бесконечного стержня напряженность в любой точке поля
имеет только радиальную составляющую Е . Следовательно потенциал будет
зависеть лишь от этой координаты и из (2.1.11) получим . Следовательно потенциал будет
зависеть лишь от этой координаты и из (2.1.11) получим
 - - = = . . (2.2.15)
Постоянную в (2.2.5) находят, положив потенциал равным нулю на некотором расстоянии L от стержня, и тогда (2.2.15)
Постоянную в (2.2.5) находят, положив потенциал равным нулю на некотором расстоянии L от стержня, и тогда
 . (2.2.16)
Лекция 2.3
Поток вектора . (2.2.16)
Лекция 2.3
Поток вектора 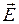 . Теорема Гаусса.
Потоком вектора . Теорема Гаусса.
Потоком вектора 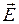 через какую-либо поверхность называется поверхностный
интеграл через какую-либо поверхность называется поверхностный
интеграл
где
Теорема Гаусса. Поток вектора напряженности электрического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на
В случае замкнутой поверхности вектор Таким образом, если силовые линии выходят из поверхности, поток будет положительным, а если входят, то – отрицательным.
Расчет электрических полей с помощью теоремы Гаусса. В ряде случаев напряженность электрического поля по теореме Гаусса рассчи- тывается достаточно просто. Однако в основе лежит принцип суперпозиции. Поскольку поле точечного заряда является центрально-симметричным, то поле центрально-симметричной системы зарядов также будет центрально-симметричным. Простейший пример – поле равномерно заряженного шара. Если распределение заряда обладает осевой симметрией, то и структура поля будет отличаться осевой симметрией. Примером может служить бесконечная равномерно заряженная нить или цилиндр. Если заряд равномерно распределен по бесконечной плоскости, то силовые линии поля будут располагаться симметрично относительно симметрии заряда. Таким образом, указанный метод расчета применяют в случае высокой степени симметрии распределения заряда, создающего поля. Далее приведем примеры расчета таких полей.
Электрическое поле однородно заряженного шара. Шар радиуса Система зарядов центрально-симметричная. В качестве поверхности интегрирования выберем сферу радиуса r (r < R), центр которой совпадает с центром симметрии заряда (см. рис.2.3.2). Рассчитаем поток вектора Вектор обладает центральной симметрией, то значение Е выбранной поверхности. Тогда
Теперь найдем заряд, заключенный внутри выбранной поверхности
В результате из (2.3.1) имеем
Далее несложно получить выражение для напряженности поля внутри шара
Отметим, что, если заряд распределен не по всему объему шара, а лишь по его поверхности (задана заряженная сфера), то напряженность поля внутри будет равна нулю.
Теперь поверхность интегрирования полностью охватывает весь заряд шара. Теорема Гаусса запишется в виде
Учтем, что поле центрально симметричное
Окончательно для напряженности поля снаружи заряженного шара получим
Таким образом, поле вне равномерно заряженного шара будет иметь такой же вид, как для точечного заряда, помещенного в центре шара. Тот же результат получим и для равномерно заряженной сферы. Проанализировать полученный результат (2.3.2) и (2.3.3) можно с помощью графика рис.2.3.4.
Электрическое поле бесконечного равномерно заряженного цилиндра. Пусть бесконечно длинный цилиндр заряжен равномерно с объемной плотностью Радиус цилиндра равен расстояния от оси. Поскольку система зарядов имеет осевую симметрию, поверхностью интегрирования мысленно выберем также цилиндр меньшего
радиуса ности и по основаниям
Из соображений симметрии следует, что
Заряд, заключенный внутри выбранного цилиндра будет равен:
Подставим оба выражения в исходную формулу теоремы Гаусса (2.3.1) После несложных преобразований получим выражение для напряженности электрического поля внутри цилиндра
В этом случае также, если заряд распределен только по поверхности цилиндра, то напряженность поля внутри равна нулю.
Теперь найдем поле снаружи заряженного цилиндра Мысленно выберем в качестве поверхности, через которую будем рассчитывать поток вектора
После несложных преобразований получим выражение для напряженности электрического поля снаружи заряженного цилиндра:
Если ввести в этой задаче линейную плотность заряда, т.е. заряд на единице длины цилиндра
Что соответствует результату, полученному с помощью принципа суперпозиции (2.2.14).
Поле бесконечной равномерно заряженной плоскости.
Видно, что силовые линии пронизывают только оба основания цилиндра. Правая часть теоремы запишется:
Внутри мысленного цилиндра будет находиться заряд равный:
Подставим оба выражения в теорему Гаусса и после несложных преобразований получим искомую функцию:
Значение напряженности поля всюду одинаковое. Силовые линии параллельны друг другу. Такое поле у которого силовая характеристика во всех точках одинакова по величине и направлению ( Теорема Гаусса в дифференциальной форме. В теории векторного поля (например, поля
Из сказанного следует Это соотношение носит название теорема Гаусса – Остроградского, оно справедливо для любого векторного поля. Тогда из (2.3.1) и (2.3.8), принимая во внимание, что заряд, заключенный в объеме V, можно записать
или, так как в обеих частях уравнения интеграл берется по одному и тому же объему,
Это уравнение математически выражает теорему Гаусса для электрического поля в дифференциальной форме. Смысл операции дивергенция состоит в том, что она устанавливает наличие источников поля (источников силовых линий). Точки, в которых дивергенция не равна нулю, являются источниками силовых линий поля. Таким образом, силовые линии электростатического поля начинаются и заканчиваются на зарядах. В заключение скажем, что в декартовой системе координат
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 13445; Нарушение авторских прав?; Мы поможем в написании вашей работы!
 ,
,
 =
= – вектор, по направлению совпадающий с нормалью к поверхности (
– вектор, по направлению совпадающий с нормалью к поверхности ( единичный вектор нормали к поверхности) и по модулю равный площади
единичный вектор нормали к поверхности) и по модулю равный площади 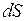 . Так как под интегралом стоит скалярное произведение векторов, то поток может получаться как положительным, так и отрицательным, в зависимости от выбора направления вектора
. Так как под интегралом стоит скалярное произведение векторов, то поток может получаться как положительным, так и отрицательным, в зависимости от выбора направления вектора 

 (в системе СИ)
(в системе СИ) . (2.3.1)
. (2.3.1)
 равномерно заряжен с объемной
равномерно заряжен с объемной  плотностью
плотностью  . Рассчитаем поле внутришара.
. Рассчитаем поле внутришара. через эту поверхность.
через эту поверхность.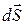 направлен по радиусу. Так как поле
направлен по радиусу. Так как поле будет одинаково во всех точках
будет одинаково во всех точках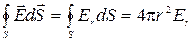 .
.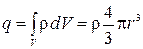 .
. .
. . (2.3.2)
. (2.3.2) Рассчитаем поле вне шара см. рис. 2.3.3.
Рассчитаем поле вне шара см. рис. 2.3.3.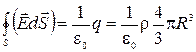 .
.
 =
= . (2.3.3)
. (2.3.3)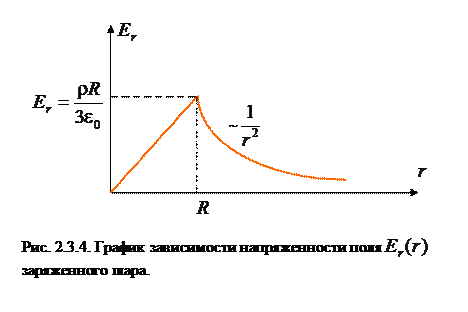

 , ось которого совпадает с осью симметрии задачи (рис.2.3.5). Рассчитаем поток
, ось которого совпадает с осью симметрии задачи (рис.2.3.5). Рассчитаем поток  .
. .
.
 .
.
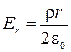 (2.3.4)
(2.3.4)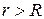 и произвольной высоты
и произвольной высоты 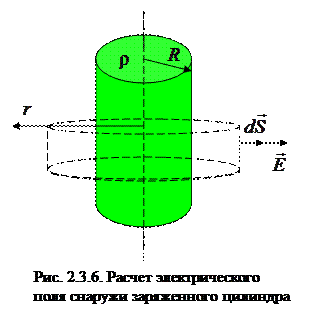 Поток
Поток 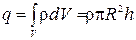 .
. . (2.3.5)
. (2.3.5)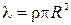 , то выражение (2.3.5) преобразуется к виду
, то выражение (2.3.5) преобразуется к виду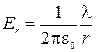 , (2.3.5а)
, (2.3.5а) Как видим зависимости в выражениях (2.3.4) и (2.3.5) разные. Построим график
Как видим зависимости в выражениях (2.3.4) и (2.3.5) разные. Построим график  .
.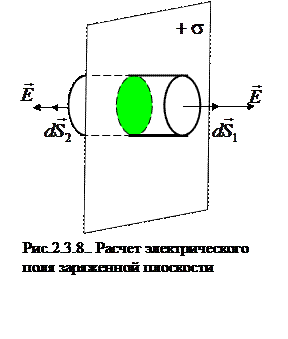 Бесконечная плоскость равномерно заряжена с поверхностной плотностью
Бесконечная плоскость равномерно заряжена с поверхностной плотностью  . Силовые линии электрического поля симметричны относительно этой плоскости, а, следовательно вектор
. Силовые линии электрического поля симметричны относительно этой плоскости, а, следовательно вектор 
 .
.
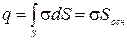 .
.
 . (2.3.6)
. (2.3.6)
 ) называют однородным.
) называют однородным. . (2.3.7)
. (2.3.7) . (2.3.8)
. (2.3.8) получим
получим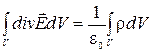
 . (2.3.9)
. (2.3.9) . (2.3.10)
. (2.3.10)