
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Электрическое поле в диэлектриках
|
|
|
|
Лекция 2.5.
Теперь рассмотрим, как изменяются характеристики электрического поля в диэлектрике. Будем рассматривать идеальный диэлектрик, т.е. такой, в котором отсутствуют свободные заряды, все заряды связаны в микроскопические нейтральные комплексы (атомы, молекулы, ионы и электроны, входящие в кристаллическую ячейку). Связанные заряды не могут удаляться друг от друга на макроскопические расстояния (эти расстояния порядка 10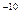 м). В первом приближении диэлектрик можно представить как совокупность микродиполей.
м). В первом приближении диэлектрик можно представить как совокупность микродиполей.
Поляризованность и связанный заряд в диэлектрике.
Главным макроскопическим электрическим свойством диэлектриков является их поляризация, которую можно характеризовать с помощью вектора поляризации или поляризованности 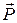 . Как всякое макроскопическое явление поляризация имеет свою микроскопическую природу. В диэлектрике либо уже имеются микродиполи (полярные молекулы, у которых «центры тяжести» положительных и отрицательных зарядов пространственно разнесены), либо они возникают под действием внешнего электрического поля, раздвигающего в разные стороны заряды разных знаков (неполярные молекулы). Поляризованность это суммарный дипольный момент в единице объема.
. Как всякое макроскопическое явление поляризация имеет свою микроскопическую природу. В диэлектрике либо уже имеются микродиполи (полярные молекулы, у которых «центры тяжести» положительных и отрицательных зарядов пространственно разнесены), либо они возникают под действием внешнего электрического поля, раздвигающего в разные стороны заряды разных знаков (неполярные молекулы). Поляризованность это суммарный дипольный момент в единице объема.
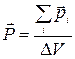 , (2.5.1)
, (2.5.1)
где 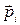 - дипольный момент микродиполя, а суммирование производится по физически бесконечно малому объему
- дипольный момент микродиполя, а суммирование производится по физически бесконечно малому объему 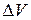 .
.
В отсутствие электрического поля диполи хаотически ориентированы в диэлектрике и его поляризованность равна нулю. При помещении диэлектрика в электрическое поле диполи определенным образом ориентируются в этом поле (см. лекцию 2.2), что приводит к возникновению в результате поляризации к не равной нулю локальной объемной 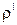 и поверхностной
и поверхностной 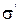 плотности связанного заряда. Однако, в диэлектриках силы притяжения между соседними микродиполями значительно слабее сил, связывающих заряды внутри диполя (при разделении диэлектрика каждый микродиполь на границе раздела не разрывается, а целиком остается в одной из частей). Поэтому любой образец диэлектрика имеет нулевой суммарный заряд:
плотности связанного заряда. Однако, в диэлектриках силы притяжения между соседними микродиполями значительно слабее сил, связывающих заряды внутри диполя (при разделении диэлектрика каждый микродиполь на границе раздела не разрывается, а целиком остается в одной из частей). Поэтому любой образец диэлектрика имеет нулевой суммарный заряд:
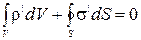 , (2.5.2)
, (2.5.2)
где V - объем образца, а S - площадь его поверхности. Поляризованность в этом случае становится отличной от нуля, она пропорциональна напряженности поля и для изотропных диэлектриков связана с ней

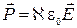 , (2.5.3)
, (2.5.3)
где 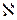 - не зависящая от напряженности величина, называемая диэлектрической восприимчивостью диэлектрика.
- не зависящая от напряженности величина, называемая диэлектрической восприимчивостью диэлектрика.
 Для получения соотношения, связывающего поляризованность с плотностью связанного заряда, рассмотрим плоский слой изотропного диэлектрика, находящийся в однородном электрическом поле
Для получения соотношения, связывающего поляризованность с плотностью связанного заряда, рассмотрим плоский слой изотропного диэлектрика, находящийся в однородном электрическом поле 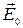 (рис.2.5.1). За счет поляризации на краях диэлектрика появляется связанный заряд с поверхностной плотностью +
(рис.2.5.1). За счет поляризации на краях диэлектрика появляется связанный заряд с поверхностной плотностью +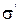 и ─
и ─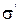 . Выделим мысленно в диэлектрике элементарный объем в виде очень тонкого цилиндра с образующими, параллельными вектору напряженности, и с основаниями площади
. Выделим мысленно в диэлектрике элементарный объем в виде очень тонкого цилиндра с образующими, параллельными вектору напряженности, и с основаниями площади 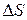 , совпадающими с поверхностями диэлектрика. Этот объем обладает дипольным моментом
, совпадающими с поверхностями диэлектрика. Этот объем обладает дипольным моментом 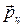 , который можно представить двумя способами. Макроскопически этот объем эквивалентен диполю, образованному зарядами +
, который можно представить двумя способами. Макроскопически этот объем эквивалентен диполю, образованному зарядами +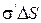 и ─
и ─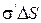 , отстоящими друг от друга на расстояние l:
, отстоящими друг от друга на расстояние l: 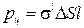 . С другой стороны этот дипольный момент можно записать как произведение поляризованности на объем выбранного цилиндра
. С другой стороны этот дипольный момент можно записать как произведение поляризованности на объем выбранного цилиндра 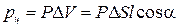 . Приравняв друг другу оба выражения, получим
. Приравняв друг другу оба выражения, получим
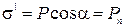 , (2.5.4)
, (2.5.4)
где 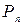 - проекция поляризованности на внешнюю по отношению к диэлектрику нормаль.
- проекция поляризованности на внешнюю по отношению к диэлектрику нормаль.
Объемную плотность связанного заряда также можно выразить через поляризованность. Для этого учтем, что по теореме Гаусса-Остроградского можно записать 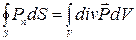 , а из (2.5.2)
, а из (2.5.2) 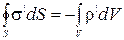 . Тогда
. Тогда 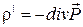 . (2.5.5)
. (2.5.5)
Таким образом, источниками линий вектора поляризованности являются связанные заряды.
Вектор электрической индукции. Теорема Гаусса для поля в диэлектрике.
Связанные заряды отличаются от сторонних тем, что не могут покинуть пределы молекул, в состав которых они входят. В остальном их свойства такие же, как и у сторонних. В частности они служат источниками электрического поля. Поэтому в формуле теоремы Гаусса (2.3.9) нужно учитывать и сторонние и связанные заряды:
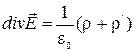 . (2.5.6)
. (2.5.6)
Тогда с учетом (2.5.5) будем иметь
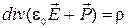 . (2.5.7)
. (2.5.7)
Выражение, стоящее в (2.5.7) в скобках обозначают обычно 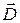 и называют электрической индукцией (или электрическим смещением). Эта величина удобна тем, что ее источниками являются только сторонние заряды, что упрощает расчет электрических полей.
и называют электрической индукцией (или электрическим смещением). Эта величина удобна тем, что ее источниками являются только сторонние заряды, что упрощает расчет электрических полей.
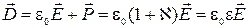 (2.5.8)
(2.5.8)
Безразмерную величину
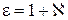 (2.5.9)
(2.5.9)
называют диэлектрической проницаемостью среды. Напомним, что мы рассматривали изотропный диэлектрик. В этом случае 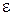 - скаляр и векторы
- скаляр и векторы  и
и 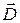 сонаправлены. В анизотропных диэлектриках диэлектрическая проницаемость – тензор, и
сонаправлены. В анизотропных диэлектриках диэлектрическая проницаемость – тензор, и  и
и 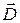 , вообще говоря, неколлинеарны.
, вообще говоря, неколлинеарны.
Единицей измерения электрической индукции в системе СИ является (Кл/м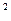 ).
).
Таким образом, для электрического поля в диэлектрике (или в общем виде) теорема Гаусса в дифференциальной форме математически может быть представлена
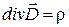 (2.5.10)
(2.5.10) 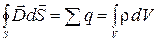 . (2.5.11)
. (2.5.11)
Поток вектора 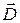 через произвольную замкнутую поверхность равен суммарному стороннем у заряду, заключенному внутри этой поверхности. Если характеризовать поле вектором
через произвольную замкнутую поверхность равен суммарному стороннем у заряду, заключенному внутри этой поверхности. Если характеризовать поле вектором  , то для поля в диэлектрике
, то для поля в диэлектрике
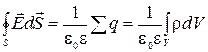 . (2.5.12)
. (2.5.12)
Из (2.5.12) следует, что напряженность поля в диэлектрике ослабевает по сравнению с вакуумом в 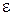 раз (то же и с потенциалом). Поэтому, например, напряженность и потенциал поля точечного заряда в диэлектрике вычисляют по формулам:
раз (то же и с потенциалом). Поэтому, например, напряженность и потенциал поля точечного заряда в диэлектрике вычисляют по формулам: 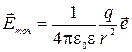 ;
; 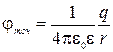 ; (2.5.13)
; (2.5.13)
напряженность поля бесконечной плоскости 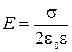 ; (2.5.14)
; (2.5.14)
электроемкость плоского конденсатора 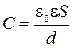 ; (2.5.15)
; (2.5.15)
и так далее.
Граничные условия для векторов 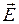 и
и 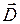 .
.
 Для общности будем полагать, что на границе двух однородных изотропных диэлектриков имеется сторонний поверхностный заряд. Пусть индукция электрического поля вблизи границы раздела в диэлектрике 1 равна
Для общности будем полагать, что на границе двух однородных изотропных диэлектриков имеется сторонний поверхностный заряд. Пусть индукция электрического поля вблизи границы раздела в диэлектрике 1 равна 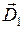 , а в диэлектрике 2 -
, а в диэлектрике 2 - 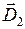 . Выберем цилиндр физически малого объема, расположив его на границе раздела диэлектриков (рис.2.5.2). Тогда можно пренебречь кривизной границы и считать поле вектора
. Выберем цилиндр физически малого объема, расположив его на границе раздела диэлектриков (рис.2.5.2). Тогда можно пренебречь кривизной границы и считать поле вектора 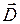 однородным в пределах сечения цилиндра, а площадь боковой поверхности считать практически равной нулю.
однородным в пределах сечения цилиндра, а площадь боковой поверхности считать практически равной нулю.
Согласно теореме Гаусса для вектора индукции можно записать (поток вектора 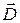 отличен от нуля только через основания цилиндра, поток через боковую поверхность равен нулю)
отличен от нуля только через основания цилиндра, поток через боковую поверхность равен нулю)
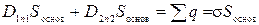 , ,
|
где 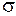 - поверхностная плотность стороннего заряда на границе раздела.
- поверхностная плотность стороннего заряда на границе раздела.
Перейдем к проекции вектора 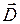 на единое к границе направление нормали
на единое к границе направление нормали 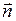 (рис.2.5.2). При этом
(рис.2.5.2). При этом  , а
, а 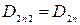 . Окончательно приходим к выражению
. Окончательно приходим к выражению
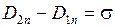 . .
| (2.5.16) |
Из этого соотношения видно, что нормальная составляющая вектора 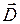 претерпевает скачок на границе раздела двух диэлектриков, однако, если на границе нет сторонних зарядов, то нормальные составляющие
претерпевает скачок на границе раздела двух диэлектриков, однако, если на границе нет сторонних зарядов, то нормальные составляющие 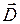 одинаковы по разные стороны границы
одинаковы по разные стороны границы
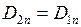 . (2.5.17) . (2.5.17)
| .13) |
 Пусть напряженность электрического поля вблизи границы раздела в диэлектрике 1 равна
Пусть напряженность электрического поля вблизи границы раздела в диэлектрике 1 равна 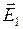 , а в диэлектрике 2 -
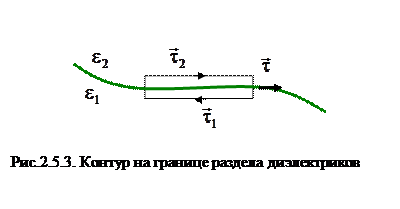
, а в диэлектрике 2 - 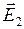 . Возьмем небольшой прямоугольный контур, ориентировав его так, чтобы две стороны были параллельны границе. Их длина настолько мала, что вдоль них можно считать электрическое поле однородным. Высота контура стремится к нулю (рис.2.5.3).
. Возьмем небольшой прямоугольный контур, ориентировав его так, чтобы две стороны были параллельны границе. Их длина настолько мала, что вдоль них можно считать электрическое поле однородным. Высота контура стремится к нулю (рис.2.5.3).
Тогда согласно теореме о циркуляции вектора 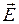
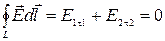 . .
|
Перейдем к проекции вектора 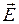 на единое направление касательной к границе раздела
на единое направление касательной к границе раздела 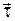 (рис.2.5.3). При этом
(рис.2.5.3). При этом 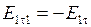 , а
, а 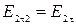 . Окончательно приходим к выражению
. Окончательно приходим к выражению
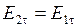 . .
| (2.5.18) |
Согласно (2.5.18) тангенциальные составляющие вектора 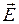 одинаковы по разные стороны границы.
одинаковы по разные стороны границы.
Согласно формулам (2.5.17) и (2.5.18) можно получить граничные условия на границе раздела диэлектриков для 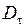 и
и 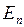 . Воспользуемся выражением
. Воспользуемся выражением 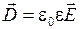 . Формулу (2.5.17) можно записать для
. Формулу (2.5.17) можно записать для 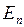
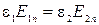
Нормальная составляющая вектора 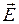 меняется скачком на границе двух диэлектриков.Формулу (2.18) можно преобразовать к виду
меняется скачком на границе двух диэлектриков.Формулу (2.18) можно преобразовать к виду 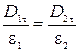

Тангенциальная составляющая вектора 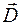 также меняется скачком на границе двух диэлектриков.
также меняется скачком на границе двух диэлектриков.
 На рисунке 2.5.4 (а, б) Показано, как меняются векторы
На рисунке 2.5.4 (а, б) Показано, как меняются векторы  и
и  при переходе через границу диэлектриков. Из рис.2.5.4. а можно записать для углов наклона силовых линий индукции и напряженности электрического поля следующие соотношения:
при переходе через границу диэлектриков. Из рис.2.5.4. а можно записать для углов наклона силовых линий индукции и напряженности электрического поля следующие соотношения:
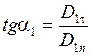 , , 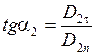 . .
|
Если на границе раздела нет сторонних зарядов и 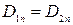 , то отношение тангенсов углов наклона силовых линий равно
, то отношение тангенсов углов наклона силовых линий равно
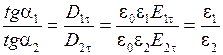 . .
| (2.5.19) |
Из полученного соотношения следует, что в диэлектрике с бớльшим значением 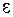 силовые линии будут составлять больший угол с нормалью к границе раздела. В случае, изображенном на рис.2.5.4,
силовые линии будут составлять больший угол с нормалью к границе раздела. В случае, изображенном на рис.2.5.4, 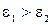 .
.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1673; Нарушение авторских прав?; Мы поможем в написании вашей работы!