Колебания. Уравнение колебаний

Лекция 2.13.

Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромеханические, электромагнитные и т.д. В зависимости от характера воздействия на колеблющуюся систему различают свободные (или собственные) колебания, вынужденные колебания, автоколебания и параметрические колебания.

Свободными (или собственными) называются такие колебания, которые происходят в системе, предоставленной самой себе после того, как ей был сообщен толчок или она была выведена из положения равновесия. Примером могут служить колебания шарика, подвешенного на нити (маятник) или прикрепленного к упругой пружине (пружинный маятник).

Вынужденными называются такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы.

Простейшими являются гармонические колебания, т.е. такие, при которых колеблющаяся величина изменяется со временем по гармоническому закону (закону синуса или косинуса). Этот вид колебаний особенно важен по двум причинам: 1) колебания в природе и технике часто имеют характер, близкий к гармоническим; 2) периодические процессы с другой зависимостью от времени могут быть представлены как наложение нескольких гармонических.

Кинематика гармонических колебаний. Уравнение колебаний.

Наименьший промежуток времени, по истечении которого колеблющаяся величина принимает первоначальное значение, называется периодом колебаний. Обозначим ее Т.

Рассмотрим систему, положение которой может быть задано с помощью одной величины, которую обозначим х. (Для примера это может быть груз, прикрепленный к пружине. Тогда х – смещение груза от положения равновесия.) Если х зависит от времени по закону

Рис. 2.9.3.

, (2.13.1)

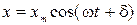
то говорят, что х совершает гармонические колебания. Здесь 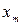- максимальное отклонение колеблющейся величины от положения равновесия, называемое амплитудой колебаний. Величину называют фазой колебаний, а ее значение в начальный момент времени, т.е. - начальной фазой. Величину, обратную периоду называют частотой колебаний, а 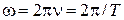- циклической или круговой частотой. Как следует из определения 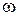, период – это время, за которое фаза изменяется на 2.

Скорость колеблющейся точки найдем дифференцированием (2.13.1) по времени

. (2.13.2)

Дифференцируя вторично, получим ускорение

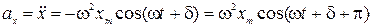(2.13.3)

или, используя (2.13.1), 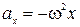. (2.13.4)

Как видно из (2.13.1), (2.13.2) и (2.13.3),фаза колебаний скорости отличается от фазы смещения на , а фаза ускорения – на . Это значит, что скорость имеет максимальное значение, когда смещение равно нулю и наоборот. Ускорение же и смещение одновременно обращаются в ноль и одновременно достигают максимума, но эти максимумы противоположных знаков.

Если полагать, для определенности, что мы рассматриваем движение груза массы на пружине, то по второму закону Ньютона

(2.13.5)

сила, действующая на тело, пропорциональна смещению и имеет противоположное направление. В случае груза на пружине это сила упругости пружины , (2.13.6) k - коэффициент упругости (или жесткости) пружины.

Необходимо отметить, что во всех случаях, когда сила, действующая на тело, имеет те же признаки, тело совершает гармонические колебания (2.13.1). Такая сила в общем случае называется квазиупругой, а уравнение движения тела имеет вид

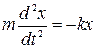(2.13.7)

или, поскольку 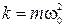, то

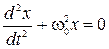. (2.13.8)

Это уравнение называется уравнением колебаний. Его решение запишется

. (2.13.9)

Если амплитуда не меняется с течением времени, то колебания будут продолжаться бесконечно долго. Такие колебания называются собственными незатухающими колебаниями. Их циклическую частоту обозначаем 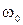. Заметим, что частота колебаний определяется из уравнения колебаний. Сведений же об амплитуде и начальной фазе из уравнения получить нельзя, их можно найти лишь, зная начальные условия, например, начальное смещение и скорость.

Энергия колебаний.

Обсудим вопрос об энергии колебаний на примере того же пружинного маятника. Эта система обладает потенциальной и кинетической энергией, которые определяются выражениями:

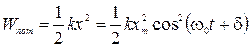, (2.13.10)

. (2.13.11)

Каждая из них меняется во времени, причем, частота их колебаний в два раза больше 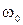. Однако, полная энергия, т.е. сумма кинетической и потенциальной, остается постоянной и равной

. (2.13.12)

Потому колебания будут незатухающими. Когда кинетическая энергия проходит через максимум, потенциальная обращается в нуль и наоборот.

Затухающие колебания.

Если кроме квазиупругой силы в системе действует сила сопротивления, пропорциональная скорости и направленная в противоположную сторону

,

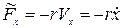то уравнение движения будет иметь вид:

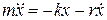(2.13.13)

или, поделив на m и введя обозначения ,

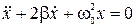. (2.13.14)

(Здесь r - постоянный коэффициент пропорциональности.)

Решение этого уравнения имеет вид

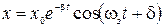, (2.13.15)

где величину называют амплитудой колебаний. Как видно амплитуда экспоненциально убывает с течением времени и колебания затухают. Коэффициент 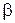называется коэффициентом затухания. Это – величина, обратная времени, в течение которого амплитуда убывает в е раз. Подставив решение в уравнение (2.13.13), получим частоту затухающих колебаний 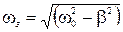. (2.13.16)

Колебания, описываемые уравнением (2.13.14), затухают потому, что система теряет энергию, совершая работу против сил сопротивления.

Вынужденные колебания. Резонанс.

Чтобы поддерживать колебания незатухающими, системе необходимо сообщить дополнительную энергию. Это можно сделать, подействовав некоторой внешней силой, причем, лучше всего гармонически меняющейся вынуждающей силой 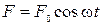. (2.13.17)

Тогда, подставив эту силу в правую часть уравнения (2.13.13) и поделив его на m, получим

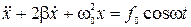, (2.13.18)

где . Решение этого уравнения будет складываться из общего решения однородного уравнения (2.13.14) и частного решения неоднородного уравнения (2.13.18). Первое слагаемое, имеющее вид (2.13.15), будет убывать и через некоторое время (время установления колебаний) станет пренебрежимо малым. Второе же слагаемое, которое и будет представлять собой вынужденные колебания, имеет вид

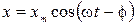. (2.13.19)

Подставив это решение в (2.13.18), получим выражение для амплитуды вынужденных колебаний

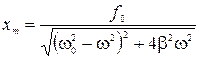(2.13.20)

и разности фаз между вынужденными колебаниями и вынуждающей силой

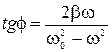. (2.13.21)

Заметим, что вынужденные колебания происходят с частотой вынуждающей силы, но отличаются от нее по фазе.

Из (2.13.20) видно, что амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы, также зависит от соотношения собственной частоты системы и частоты вынуждающей силы. При некоторой определенной для данной системы частоте вынуждающей силы амплитуда колебаний достигает максимального значения. Это явление называется резонансом, а соответствующая частота – резонансной частотой. Расчет дает 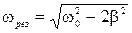, (2.13.22)

а при малом затухании 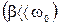резонансная частота примерно равна собственной.

Дата добавления: 2014-01-07