Аналитическое решение задачи наведения

Способы решения задачи наведения

Для метода "Параллельное сближение" задачу наведения можно решить следующими способами:

- аналитическим;

- графическим;

- инструментальным;

- глазомерным;

- автоматизированным.

Все перечисленные способы, кроме аналитического, позволяют решить задачу с меньшей затратой времени и достаточной степенью точности вывода истребителя в точку встречи с воздушной целью.

Для ОБУ решение задачи наведения любым способом состоит главным образом в определении курса и времени полета истребителя до точки встречи с воздушной целью (точки С) и положения этой точки.

Сущность способа заключается в определении, путем математических вычислений, искомых величин:

- курса истребителя (Ки) в точку встречи;

- точки встречи истребителя с целью (С), ее азимут и дальность (Аз, Д);

- времени полета истребителя (t и) до точки встречи.

Исходными данными для решения задачи наведения аналитическим способом являются:

- скорость цели (Vц);

- исходная дальность между истребителем и целью (До);

- курсовой угол истребителя (Yи);

- пеленг цели (Пц);

- скорость истребителя (Vи).

Все эти данные, кроме скорости истребителя, ОБУ может определить на экране ИКО. Скорость истребителя ОБУ задает в зависимости от параметров полета цели и исходного положения цели и истребителя.

а) Определение курса полета истребителя

Курс полета истребителя определим, воспользовавшись рисунком 3.1.:

Ки = Пц + Yц (3.1)

Зная скорости движения истребителя и воздушной цели, а также значение курсового угла истребителя, определим курсовой угол цели. Из треугольника ЦСИ (рис. 3.1.) по теореме синусов имеем:

;

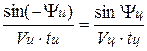откуда sin Yц = , т.к. t и = t ц по условию.

Окончательно получим:

sin Yц = – n × sin Yи (3.2)

где n =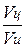

Величину курсового угла воздушной цели для расчета курса полета истребителя можно определить на навигационной линейке НЛ-10М по ключу, который показан на рисунке 3.3. При этом следует иметь в виду, что углы Yц и Yи имеют разные знаки.

Рис. 3.3.Определение на НЛ-10М величины курсового угла ВЦ

Знак величины курсового угла воздушной цели указывает на сторону наведения истребителя. При наведении истребителя слева от воздушной цели курсовой угол цели отрицательный, справа – положительный.

Пример №1:

- скорость полета воздушной цели V ц = 760 км/ч,

- скорость полета истребителя V и = 950 км/ч,

- курсовой угол истребителя Yи = – 30°,

- пеленг воздушной цели П ц = 60°.

Определить курсовой угол воздушной цели (Y ц) и курс истр. (К и).

Решение:

1. Установить визирку НЛ-10М на деление 95 шкалы 5.

2. Подвести под черту визирки деление 30 шкалы 3.

3. Передвинуть визирку на деление 76 шкалы 5.

4. Против черты визирки на шкале 3 отсчитать Y ц (Y ц = 24°).

5. По формуле (3.1) определить курс истребителя:

К и = 60° + 24° = 84°.

б) Определение положения точки встречи

Положение точки встречи (точки С) удобно определить, отложив от точки местоположения воздушной цели (точки Ц) (рис. 3.1.) в направлении ее полета длину пути цели (S ц) до точки встречи.

Чтобы определить длину пути цели (S ц) воспользуемся теоремой синусов. Из треугольника ЦСИ (рис. 3.1.) имеем:

откуда:

Sц = Д₀ 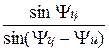(3.3)

Курсовой угол цели (Yц) определяется по формуле (3.2) или на НЛ-10М по ключу (рис. 3.3.).

Длину пути, пройденного целью (S ц) до точки встречи, можно определить с использованием НЛ-10М по ключу, который показан на рисунке 3.4.:

Рис. 3.4.Определение на НЛ-10М длины пути, пройденного целью

до точки встречи

Пример № 2: Определить путь, пройденный целью до точки встречи, используя условия примера № 1: Yи = – 30°, Y ц = 24°, для исходной дальности (До), равной 120 км, т.е. До = 120 км.

Решение:

1. Установить визирку НЛ-10М на деление 120 шкалы 5;

2. Подвести под черту визирки деление Y ц –Y и = 54°,

т.к. Y ц – Y и = 24° – (– 30°) = 24° + 30° = 54°;

3. Передвинуть визирку на деление 24 шкалы 3;

4. Против черты визирки на шкале 5 отсчитать S ц (S ц = 60 км).

в) Определение времени полета истребителя

Зная путь цели, легко найти время полета цели и истребителя до точки встречи: tц = S ц/V ц

Время полета цели и истребителя до точки встречи можно определить на навигационной линейке НЛ-10М по ключу, который показан на рисунке 3.5.

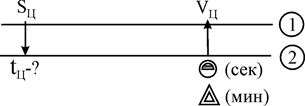
Рис. 3.5.Определение на НЛ-10М времени полета цели до точки встречи

Пример № 3: Используя условия примеров № 1 и № 2, определить время полета воздушной цели или истребителя до точки встречи.

Решение:

1. Подвести красный треугольный индекс шкалы 2 под деление 76 шкалы 1

2. Против деления 60 отсчитать время полета t = 4 мин 50 сек

Обращаясь к рисунку 3.2., можно сделать вывод, что при одной и той же исходной дальности (До), минимальное значение времени сближения будет при полете воздушной цели и истребителя на встречных курсах, когда Yи = 0, а максимальное – при полете на попутных курсах (при догоне цели, когда Y и = 180°).

Дата добавления: 2014-01-07