Устойчивость импульсных систем

Динамические свойства импульсных систем с амплитудной модуляцией во многом аналогичны динамическим свойствам непрерывных систем. Поэтому и методы анализа таких систем являются аналогами соответствующих методов исследования непрерывных систем.

Устойчивость импульсных систем управления, как и устойчивость непрерывной системы, определяется характером ее свободного движения. Импульсная система устойчива, если свободная составляющая переходного процесса 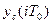с течением времени затухает, т. е. если

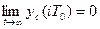(3.56)

Свободная составляющая 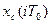является решением однородного разностного уравнения:

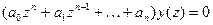(3.57)

где 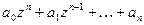- характеристическое уравнение, представляющее знаменатель дискретной передаточной функции:

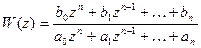(3.58)

Решение уравнения (56) представляет собой сумму

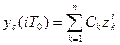, (3.59)

где 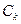- постоянные интегрирования, зависящие от начальных условий; 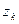- корни характеристического уравнения

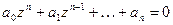
Из выражения (59) видно, что при 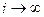решение 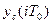стремится к нулю лишь в том случае, если все корни 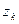по модулю меньше единицы, т. е. если

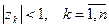(3.60)

Отсюда можно сформулировать общее условие устойчивости: для устойчивости импульсной системы необходимо и достаточно, чтобы все корни характеристического уравнения системы находились внутри круга единичного радиуса с центром в начале координат (рис. 3.34.).

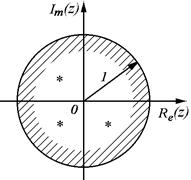
Рис. 3.34.

Если хотя бы один корень 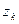располагается на окружности единичного радиуса, то система находится на границе устойчивости. При 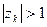система неустойчива.

Таким образом, единичная окружность в плоскости корней z_k является границей устойчивости _, следовательно, играет такую же роль, как и мнимая ось в плоскости корней 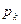(рис. 3.35.)

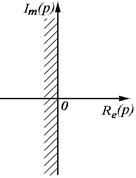
Рис. 3.35.

Этот вывод вытекает также из основной подстановки метода z -преобразования:

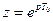
Действительно, пусть 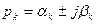, тогда

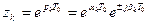(3.61)

и требование 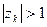сводится к неравенству

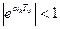(3.62)

откуда следует известное в теории непрерывных систем условие сходимости:

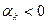(3.63)

Аналогично непрерывным системам устойчивость импульсных систем может определена с помощью специальных правил - критериев.

Дата добавления: 2014-01-07