Высшие гармоники

ПУЛЬСАЦИИ ВЫПЯМЛЕННГО НАПРЯЖЕНИЯ

Определим переменные составляющие выпрямленного напряжения трёхфазных выпрямителей. Всякая переменная составляющая, как любая периодическая функция, может быть представлена в виде суммы синусоид высших гармоник с убывающей амплитудой (ряд Фурье). Амплитудное значение напряжения гармоники зависит от выходного напряжения выпрямителя, числа пульсов, угла регулирования тиристоров в управляемом выпрямителе и номера гармоники, и может быть определено по формуле:

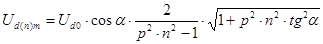, (6.1)

где U _d0 – напряжение холостого хода выпрямителя;

р – число пульсов выпрямленного напряжения;

n – номер гармоники;

a - угол регулирования тиристоров управляемого выпрямителя (для выпрямителя на диодах a = 0).

Действующее значение напряжения гармоники будет меньше амплитудного в 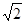раз и составит:

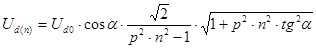, (6.2)

Отношение действующего значения напряжения гармоники к напряжению холостого хода выпрямителя

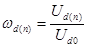(6.3)

называется коэффициентом волнистости n -ой гармоники. При a = 0 и g = 0 .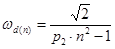

В табл. 6.1 приведены значения коэффициентов волнистости 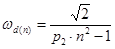для шести и двенадцати пульсовых трёхфазных выпрямителей.

Таблица 6.1

Коэффициенты волнистости для шести и двенадцати пульсовых

трёхфазных выпрямителей

Схема выпрямителя	6-ти пульсовая	12-ти пульсовая
Номер гармоники n
Частота гармоники f, Гц
Коэффициент волнистости	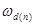0,0404	0,0099	0,0044	0,0099	0,00025	0,00011
Коэффициент полной волнистости	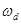0,042	0,0143

Как следует из выражения (6.1), наибольшую амплитуду имеет первая гармоника выпрямленного напряжения.

Кроме отдельных коэффициентов волнистости для каждой гармоники применяется коэффициент полной волнистости, учитывающий все гармоники:

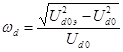, (6.4)

где U _doэ – эффективное значение выпрямленного напряжения (см. пункт 3.2).

Очевидно, что коэффициент полной волнистости больше, чем коэффициент волнистости первой гармоники .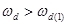

С ростом тока нагрузки, когда угол коммутации вентильных токов g > 0, и в управляемых выпрямителях при a > 0, коэффициенты волнистости возрастают.

Указанные значения коэффициентов волнистости вычислены при условии, что фазные напряжения питающей сети симметричны. Если же из-за больших однофазных нагрузок симметрия напряжений питающей сети нарушается, то в 6-ти пульсовых выпрямителях кроме гармоник с частотами 300, 600 и 900 Гц появляется гармоника с частотой 100 Гц. Из-за взаимодействия с основными гармониками появляются комбинационные гармоники:

1. 300 – 100 = 200 Гц – разностная частота первой гармоники и гармоники 100 Гц;

2. 300 + 100 = 400 Гц – суммарная частота первой гармоники и гармоники 100 Гц;

3. 600 – 100 = 500 Гц – разностная частота второй гармоники и гармоники 100 Гц.

Напряжения комбинационных гармоник более высоких порядков обычно невелики, и ими пренебрегают.

Дата добавления: 2014-01-07