Оценка апостериорной погрешности

Мы записывали априорные оценки главного члена погрешности в виде R ₀ = Ah ^p, (1) где A – коэффициент, зависящий от метода интегрирования и вида подинтегральной функции; h – шаг интегрирования, p – порядок метода. Такого сорта оценку можно применить не только к методам интегрирования, но и ко многим другим численным алгоритмам.

Первая формула Рунге.

Пусть w – точное значение, к которому должен прийти численный метод (мы его не знаем). Результат численного расчета дает нам величину w_h такую, что . (2)

Теперь вычислим ту же величину w с шагом kh, где константа k может быть как больше, так и меньше единицы. Коэффициент A будет одинаковый, так как вычисление осуществляется одним и тем же методом. Получаем . (3)

Приравняем правые части выражений (2) и (3) и пренебрежем бесконечно малыми величинами одинакового порядка малости.

. Отсюда, учитывая (1), получим . (4) Эта формула, выражающая апостериорную оценку главного члена погрешности величины w путем двойного просчета с разным шагом, носит название первой формулы Рунге. При уменьшении шага главный член погрешности будет стремиться к полной погрешности R.

Вторая формула Рунге.

Так как модуль и знак апостериорной погрешности из формулы (4) известны, можно уточнить искомое значение 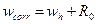. Это вторая формула Рунге. Однако теперь погрешность w _corr не определена, известно лишь, что она по модулю меньше R ₀.

Алгоритм Эйткена.

Способ оценки погрешности для случая, когда порядок метода p неизвестен. Более того, алгоритм позволяет опытным путем определить и порядок метода. Для этого в третий раз вычислим значение величины w с шагом k ² h:

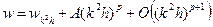. (5)

Приравняем правые части выражений (5) и (3): 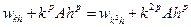. Отсюда:

. Подставим сюда значение R ₀ из (4):

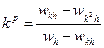. Из этой формулы определяем знаменатель для (4). Кроме того, определяем порядок . Для правильно реализованных алгоритмов методов априорных и апостериорных порядки должны получиться совпадающими. Программная реализация формул Рунге позволяет вычислить определенные интегралы с заданной точностью, когда выбор необходимого числа разбиений интервала интегрирования осуществляется автоматически. Пример – уже рассмотренная ранее формула Ромберга.

Дата добавления: 2014-01-07