Алгоритм выполнения отдельного шага

Рассмотрим более детально логику каждого из четырех циклов обработки одного 512-битного блока. Каждый цикл состоит из 16 шагов, оперирующих с буфером ABCD. Каждый шаг можно представить в виде:

(B + CLS_S (A + f (B, C, D) + X[k] + T[i])) → A

где: A, B, C, D – четыре слова буфера; после выполнения каждого отдельного шага происходит циклический сдвиг влево на одно слово;

f – одна из элементарных функций f_F, f_G, f_H, f_I;

X [k] - k – ое 32- битовое слово в q – ом 512 блоке сообщения;

CLS_s – циклический сдвиг влево на s битов 32-битного аргумента;

T [i] – i-ое 32-битное слово в матрице Т;

+ - сложение по модулю 2³².

Схема выполнения отдельного шага алгоритма

На каждом из четырех циклов алгоритма используется одна из четырех элементарных логических функций. Каждая элементарная функция получает три 32-битных слова на входе и на выходе создает одно 32-битное слово. Каждая функция является множеством битовых логических операций, т.е. n- ый бит выхода является функцией от n -ого бита трех входов. Элементарные функции следующие:

f_F = (B & C) v (not B & D)

f_G = (B & D) v (C & not D)

f_H = B Å C Å D

f_I = C Å (B & not D)

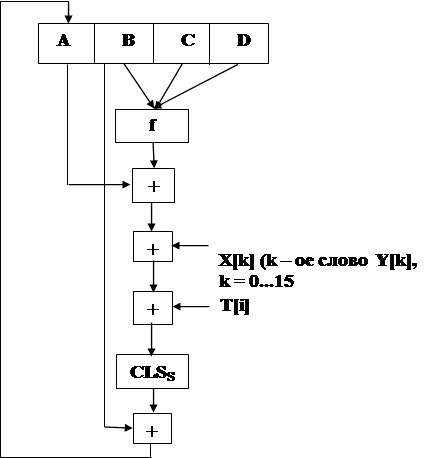Рис. 9.6. Схема выполнения отдельного шага

алгоритма MD5

Массив из 32-битных слов X [0..15] содержит значение текущего 512-битного входного блока, который обрабатывается в настоящий момент. Каждый цикл выполняется 16 раз, а так как каждый блок входного сообщения обрабатывается в четырех циклах, то в результате получается, что каждый блок входного сообщения обрабатывается 64 раза по схеме, показанной на рисунке 9.6. Если представить входной 512-битный блок в виде шестнадцати 32-битных слов, то каждое входное 32-битное слово используется четыре раза, по одному разу в каждом цикле, и каждый элемент таблицы Т, состоящей из 64 32-битных слов, используется только один раз. После каждого шага цикла происходит циклический сдвиг влево четырех слов A, B, C и D. На каждом шаге изменяется только одно из четырех слов буфера ABCD. Следовательно, каждое слово буфера изменяется 16 раз, и затем 17-ый раз в конце для получения окончательного выхода данного блока.

Можно суммировать алгоритм MD5 следующим образом:

MD₀ = IV

MD_q+1 = MD_q + f_I[Y_q, f_H[Y_q, f_G[Y_q, f_F[Y_q, MD_q]]]]

MD = MD_L-1

где: IV – начальное значение буфера ABCD, определенное на шаге 3;

Y_q – q-ый 512-битный блок сообщения;

L – число блоков в сообщении (включая поля дополнения и длины);

MD – окончательное значение дайджеста сообщения.

Алгоритм MD5 имеет следующее свойство: каждый бит хэш-кода является функцией от каждого бита входа. Комплексное повторение элементарных функций f_F, f_G, f_H и f_I обеспечивает то, что результат хорошо перемешан; то есть маловероятно, чтобы два сообщения, выбранные случайно, даже если они имеют явно похожие закономерности, имели одинаковый хэш-код. Считается, что MD5 является наиболее сильной хэш-функцией для 128-битного хэш-кода, то есть трудность нахождения двух сообщений, имеющих одинаковый дайджест, имеет порядок 2⁶⁴ операций. В то время, как трудность нахождения сообщения с данным дайджестом имеет порядок 2¹²⁸ операций.

Дата добавления: 2014-01-07