Функция, реализующая операцию ОБЪЕДИНИТЬ

Begin

Функция для построения оптимального дерева двоичного поиска.

End

End

Begin

Begin

Begin

Алгоритм динамического программирования нахождения корней оптимальных поддеревьев.

1. for i=0 until n do

2. w_ii=q_i

3. c_ii=0

end;

4. for l= 1 until n do

5. for i=0 until n–l do

6. j=i+l;

7. w_ij = w_i,j–1 + p_j + q_j;

8. пусть m – значение k, i < k £ l, для которого сумма c_i,k–1+c_kj минимальна;

9. c_ij = w_i,j + c_i,m–1+c_mj;

10. r_ij=a_m,

2. После вычисления всех r _ij вызывается функция BuildTree (0, п) для рекурсивного построения оптимального дерева для T _0n.

BuildTree(i, j):

образовать корень vij дерева Tij;

пометить vij меткой rij;

пусть m – индекс числа rij (т. е. rij=am);

if i<m–1 then сделать BuildTree(i, m–1) левым поддеревом узла vij;

if m<j then сделать BuildTree(т, j) правым поддеревом узла vij

end \ ÿ

Пример 3.4. Рассмотрим четыре элемента а ₁ <а ₂ <а ₃ <а ₄ с q ₀ =1/8, q ₁ =3/16, q ₂ = q ₃ = q ₄ =1/16 и p ₁= 1/4, p ₂= 1/8, p ₃= p ₄= 1/16. В таблице даны значения w _ij, r _ij и c _ij, вычисленные приведенным алгоритмом нахождения корней оптимальных поддеревьев. Для удобства записи значения w _ij и c _ij в этой таблице были умножены на 16.

Таблица 10: Значения w _ij, r _ij и c _ij

w 00= 2 c 00= 0	w 11= 3 c 11= 0	w 22= 1 c 22= 0	w 33= 1 c 33= 0	w 44= 1 c 44= 0
w 01= 9 c 01= 9 r 01= a 1	w 12= 6 c 12= 6 r 12= a 2	w 23= 3 c 23= 3 r 23= a 3	w 34= 3 c 34= 3 r 34= a 4
w 02= 12 c 02= 18 r 02= a 1	w 13= 8 c 13= 11 r 13= a 2	w 24= 5 c 24= 8 r 24= a 4
w 03= 14 c 03= 25 r 03= a 1	w 14= 10 c 14= 18 r 14= a 2
w 04= 16 c 04= 33 r 04= a 2

Например, чтобы вычислить r ₁₄, надо сравнить значения c ₁₁+ c ₂₄, c ₁₂+ c ₃₄ и c ₁₃+ c ₄₄, равные (после умножения на 16) соответственно 8, 9 и 11. Таким образом, в строке 8 алгоритма k=2 дает минимум, так что r ₁₄ =a ₂.

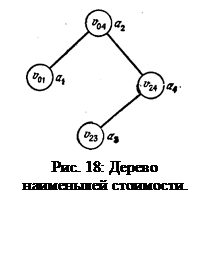
Заполнив таблицу 10, строим дерево Т ₀₄, вызывая BuildTree (0, 4). На рис. 18 изображено полученное в результате дерево двоичного поиска. Его стоимость равна 33/16. ÿ

Теорема 12. Алгоритм 15 строит оптимальное дерево двоичного поиска за время O(n³).

Доказательство. Вычислив таблицу значений r _ij, по ней строят оптимальное дерево за время О(п), вызывая процедуру BuildTree. Эта процедура вызывается только п раз, и каждый вызов занимает постоянное время.

Наиболее дорого стоит алгоритм динамического программирования. Строка 8 находит значение k, минимизирующее c _i,k–1+ c _kj, за время O (j – i). Остальные шаги цикла в строках 5–10 занимают постоянное время. Внешний цикл в строке 4 выполняется п раз, внутренний – не более п раз для каждой итерации внешнего цикла. Таким образом, суммарная сложность составляет 0(п³).

Что касается корректности алгоритма, то простой индукцией по l=j–i можно показать, что r _ij и c _ij правильно вычисляются в строках 9 и 10.

Чтобы показать, что оптимальное дерево правильно строится процедурой BuildTree, заметим, что если v _ij – корень поддерева для { a _i+1, a _i+2, ¼, a _j}, то его левый сын будет корнем оптимального дерева для { a _i+1, a _i+2, ¼, a _m–1}, где r _ij= а _m, а правый будет корнем оптимального дерева для { a _m+1, a _m+2, ¼, a _j}.

Теперь должно быть ясно, как доказать по индукции, что процедура BuildTree (i, j) правильно строит оптимальное дерево для { a _i+1, a _i+2, ¼, a _j}. ÿ

В алгоритме 15 можно ограничить поиск т в строке 8 областью между положениями корней деревьев T _i,j–1 и T _i+1,j, при этом гарантируется нахождение минимума. Тогда алгоритм 15 сможет находить оптимальное дерево за время 0(п²).

3.6. Простой алгоритм для нахождения объединения непересекающихся множеств

Часто во многих приложениях возникают задачи, которые имеют дело с непересекающимися множествами, содержащими счетные количества элементов, в которых нужно бывает отыскивать какие-то элементы и объединять различные множества. Тогда задача преобразования множеств обладает следующими тремя особенностями.

1. Всякий раз сливаются только непересекающиеся множества.

2. Элементы множеств можно считать целыми числами от 1 до п.

3. Операциями над множествами являются ОБЪЕДИНИТЬ и НАЙТИ.

Изучим структуры данных для задач такого типа. Пусть даны п элементов, которые будут считаться целыми числами 1, 2, ¼, п. Предположим, что вначале каждый элемент образует одноэлементное множество. Пусть надо выполнить последовательность операций ОБЪЕДИНИТЬ и НАЙТИ. Напомним, что операция ОБЪЕДИНИТЬ имеет вид Union (A, B, C), указывающий, что два непересекающихся множества с именами А и В надо заменить их объединением и назвать это объединение С. В приложениях часто неважно, что выбирается в качестве имени множества, так что будем предполагать, что множества можно именовать целыми числами от 1 до п. Кроме того, будем предполагать, что никакие два множества ни в один момент не названы одинаково.

Эту задачу позволяют решить несколько интересных структур данных. В этом разделе познакомимся со структурой данных, благодаря которой можно выполнить за время О (п log п) последовательность, содержащую до п–1 операций ОБЪЕДИНИТЬ и до О (п log п) операций НАЙТИ. В следующем разделе будет описана структура данных, позволяющая обрабатывать последовательность из 0(п) операций ОБЪЕДИНИТЬ и НАЙТИ в худшем случае за время, почти линейное по n. Эти структуры данных могут обрабатывать последовательности операций ВСТАВИТЬ, УДАЛИТЬ и ПРИНАДЛЕЖАТЬ с той же вычислительной сложностью.

Заметим, что в алгоритмах поиска, изложенных в разд. 3.2-3.5, предполагалось, что элементы выбираются из универсального множества, много большего, чем множество выполняемых операций. В этом разделе универсальное множество будет приблизительно того же размера, что и длина последовательности выполняемых операций.

По-видимому, простейшей структурой данных для задачи типа ОБЪЕДИНИТЬ – НАЙТИ служит массив, представляющий набор множеств в данный момент. Пусть R – массив размера п, a R [ i ] – имя множества, содержащего элемент i. Так как вид имен множеств не существен, можно вначале взять R [ i ] =i, l £ i £ n, и выразить тем самым факт, что перед началом работы набором множеств является {{1}, {2}, ¼, { п }} и множество { i } имеет имя i.

Операция Find (i) выполняется путем печати значения R [ i ] в данный момент. Поэтому сложность выполнения операции НАЙТИ постоянна, а это лучшее, на что можно надеяться.

Чтобы выполнить операцию Union (A, B, C), надо последовательно просмотреть массив R и заменить каждую его компоненту, равную А или В, на С. Поэтому сложность выполнения такой операции есть О (п). Последовательность из п операций ОБЪЕДИНИТЬ могла бы потребовать О (п ²) времени, что нежелательно.

Этот безыскусный алгоритм можно улучшить несколькими способами. Для одного улучшения можно воспользоваться преимуществом связанных списков. Для другого – понять, что всегда эффективнее влить меньшее множество в большее. Чтобы сделать это, надо отличать "внутренние имена", используемые для идентификации множеств в массиве R, от "внешних имен", упоминаемых в операциях ОБЪЕДИНИТЬ. И те, и другие предполагаются числами от 1 до п, но не обязательно одинаковыми.

Рассмотрим следующую структуру данных для этой задачи. Как и ранее, возьмем такой массив R, что R [ i ] содержит "внутреннее" имя множества, которому принадлежит элемент i. Но теперь для каждого множества А можно построить связанный список List [ A ], содержащий его элементы. Для реализации этого связанного списка применяются два массива List и Next. List [ A ] представляет собой целое число j, указывающее, что j – первый элемент в множестве с внутренним именем A. Next [ j ] дает следующий элемент в А, Next [ Next [ j ]] – следующий за ним элемент, и т. д.

Кроме того, возьмем еще массив, называемый Size (РАЗМЕР), такой, что Size [ A ] – число элементов в множестве А. Множества будут переименовываться по внутренним именам, а два массива In_Name (Внутреннее имя) и Out_Name (Внешнее имя) будут устанавливать соответствие между внутренними и внешними именами. Иными словами, Out_Name[ А ] – это настоящее имя (диктуемое операциями ОБЪЕДИНИТЬ) множества с внутренним именем А. In_Name[ j ] – это внутреннее имя множества с внешним именем j. Внутренние имена – это имена, используемые в массиве R.

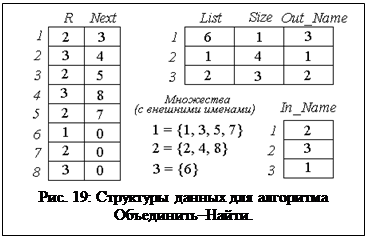
Пример 3.5. Пусть n=8 и у нас есть набор из трех множеств {1, 3, 5, 7}, {2, 4, 8} и {6} с внешними именами 1, 2 и 3 соответственно. Структуры данных для этих трех множеств показаны на рис. 19, где 2,3 и 1 — внутренние имена для 1,2 и 3 соответственно. ÿ

Операция Find (i) выполняется, как и раньше, обращением к R [ i ] для установления внутреннего имени множества, содержащего элемент i в данный момент. Затем Out_Name[ R [ i ]] дает настоящее имя множества, которому принадлежит i.

Операцию объединения вида Union(I, J, K) выполняется с помощью алгоритма 16. (Номера строк относятся к процедуре алгоритма).

Алгоритм 16. Реализация операции ОБЪЕДИНИТЬ

1. Определяем внутренние имена для множеств I и J (строки 1, 2).

2. Сравниваем относительные размеры множеств I и J, справляясь в массиве Size (строки 3, 4).

3. Проходим список элементов меньшего множества и изменяем соответствующие компоненты в массиве R на внутреннее имя большего множества (строки 5–9).

4. Вливаем меньшее множество в большее, добавляя список элементов меньшего множества к началу списка для большего множества (строки 10–12).

5. Присваиваем полученному множеству внешнее имя К (строки 13, 14).

Вливая меньшее множество в большее, мы делаем время выполнения операции ОБЪЕДИНИТЬ пропорциональным мощности меньшего множества. Все детали приведены в процедуре алгоритма.

Union(I, J, K)

Дата добавления: 2014-01-07