Лекция 28

МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ

Этот метод является одним из наиболее распространенных и точных методов (предложен Р. Фишером в 1912 г.). Если наработка на отказ изделия выражается к виде плотности распределения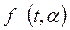, то функция максимального правдоподобия запишется в виде произведения плотностей вероятностей

В случае, если наработка на отказ представляет собой дискретную величину и принимает значения Т₁, Т₂,..., Т_n соответственно с вероятностями Р₁(α), Р₂(α),..., Р и 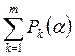, т. е. функция правдоподобия выражается зависимостью вида

Суть метода максимального правдоподобия состоит в том, что в качестве оценок параметра α принимают такое его значение, при котором функция правдоподобия принимает наибольшее значение. Поскольку функции L и lпL достигают экстремума при одном и том же значении параметра α, то эти критические значения α определяются из уравнения правдоподобия

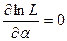
Если наработку на отказ изделия выражают через плотность вероятности, зависящую от нескольких неизвестных параметров то для их нахождения составляют столько уравнений правдоподобия, сколько неизвестных параметров. Для плотности распределения наработки на отказ с двумя неизвестными параметрами составляется два уравнения правдоподобия и решают их относительно неизвестных:

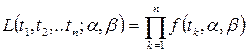
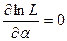
Оценки параметров, полученные методом максимального правдоподобия, являются состоятельными, эффективными и имеют минимальную дисперсию.

Рассмотрим применение метода максимального правдоподобия для непрерывного распределения с одним неизвестным параметром. Из непрерывных распределений наиболее употребительно - показательное.

Пример. Предположим, что проводят испытания на долговечность n изделий. Эти испытания прекращают, если все изделия отказали. Времена наработки до отказа изделий обозначим.через Т₁, Т₂,..., Т_n. Допустим, что время наработки до отказа имеет показательное распределение с плотностью вероятности вида

где Т = 1 / λ - среднее значение наработки на отказ.

Функцию правдоподобия запишем в виде

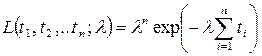
или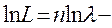

Найдем частную производную от данной функции по параметру λ:

Предположив, что , получим

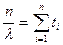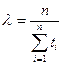, , Т =1/n ·

Метод максимального правдоподобия применим и к дисретным распределениям.

ОЦЕНКА ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ МЕТОДОМ ПРИРАВНИВАНИЯ МОМЕНТОВ

Метод моментов является самым общим методом точечной оценки неизвестных параметров распределения (предложен К. Пирсоном). Этот метод нашел широкое применение в статистике, поскольку он позволяет довольно просто получить результаты без использования вычислительной техники, в то время как метод максимального правдоподобия требует громоздких вычисле- ний на ЭВМ.

Суть этого метода состоит в том, чтобы приравнять выборочное среднее значение параметра и его дисперсию к среднему значению и дисперсии теоретической функции распределения.

Математически это можно записать так:

;

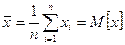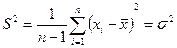
В зависимости от того, сколько неизвестных параметров входит в предполагаемую теоретическую функцию распределения, берут такое же число уравнений. Для получения оценок параметров распределения составляют столько уравнений, сколько неизвестных параметров. Оценки, получаемые с помощью метода моментов, не являются наилучшими с точки зрения их эффективности. Однако их можно использовать в качестве первых приближений. Рассмотрим на примере нахождение оценок параметров распределения методом моментов.

Пример. Испытаниям подвергалось десять домкратов, причем испытания проводились до отказа каждого домкрата при наработках 50, 60, 70, 75, 80, 85, 90, 95, 100, 110 ч. Предположим, что наработку до отказа можно описать законом гамма-распределения с плотностью вероятности:

Найти оценки параметров распределения.

Р е ш е н и е. Для определения оценок параметров распределения воспользуемся методом моментов. Для этого найдем среднее значение параметра и его среднее квадратическое отклонение по результатам испытаний:

ч

ч²

Математическое ожидание для гамма-распределения М[t]= α / λ. Дисперсия выражается зависимостью вида σ² = α / λ². Приравняем теоретические и статистические значения и найдем оценки параметров:

α / λ. = t¯= 81,5; α / λ² = 338

После вычисления получим α = 19,65, λ = 0,24.

ДОВЕРИТЕЛЬНЫЕ ПРЕДЕЛЫ ДЛЯ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ

Ранее были рассмотрены методы нахождения оценок параметров распределения. Однако какими бы хорошими свойствами эти оценки не обладали все-таки бывает недостаточным характеризовать качество и надежность изделий только с помощью оценок. Следует отметить, что оценки максимального правдоподобия обычно сходятся нормальному распределению при увеличении объема выборки. Пусть γ — установленный доверительный уровень. Поставим задачу определить интервал значений параметра λ, границы торого лежат в пределах _λ, λ¯.

Двусторонним доверительным интервалом для параметра λ с коэффициентом доверия γ называют случайный интервал, который обладает тем свойством, что

Р = (_λ < λ < λ¯) = γ

Отсюда верхняя граница для параметра λ определяется по формуле

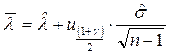
Аналогично нижняя доверительная граница будет равна

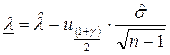
где 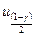- квантиль функции нормального распределения берется из табл. 1 приложения;. — оценка среднего квадратического отклонения; п - объем выборки.

Дисперсия оценки максимального правдоподобия

где L — функция максимального правдоподобия; λ — оцениваемый параметр.

Таким образом, полученные доверительные границы оценок параметров распределения могут быть использованы при нахождении доверительных границ функции надежности их подстановкой в эту функцию, если она зависит от одного неизвестного параметра. В том же случае, если функции надежности зависит от двух или большего числа параметров, то мы можем найти ее точечную оценку, подставив точечные оценки неизвестных параметров в функцию надежности. В общем случае, когда имеется более одного неизвестного параметра, нельзя подставлять доверительные пределы данных параметров непосред- ственно в выражение надежности с целью получения доверительного интервала последней.

Если можно найти среднее значение и дисперсию оценки надежности, то приближенные доверительные пределы функции надежности получим, воспользовавшись общей закономерностью, согласно которой при большом объеме выборки оценка надежности распределена по закону, близкому к нормальному. Для, этого находят среднее значение оценки надежности и ее дисперсию, а затем определяют доверительные пределы так же, как и для параметров нормального распределения. Подробно о нахождении нижней доверительной границы для функции надежности изложено в подразделе 9.3.

Дата добавления: 2014-01-07