Вопрос 8: средняя и предельная ошибки выборки

При проведении любых статистических исследований (сплошных и выборочных) нельзя получить абсолютно точные данные, т. к. возникает ошибка выборки. Для выборочных обследований характерны ошибки репрезентативности (это отклонение значения показателя обследованной совокупности от его величины в генеральной совокупности). Введём условные обозначения:

· N – объём генеральной совокупности;

· n – число единиц в выборочной совокупности;

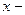· количественное значение признака в выборочной совокупности;

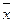· - среднее значение признака;

· p – доля признака в выборочной совокупности;

· σ – среднее квадратическое отклонение;

· σ² – дисперсия;

· μ_p – средняя ошибка выборки для доли;

· μ_x - средняя ошибка выборки для количественных признаков;

· Δ_p – предельная ошибка выборки для доли;

· Δ_x – предельная ошибка выборки для количественных признаков;

· t – коэффициент доверия;

· Р – вероятность.

Ошибки выборки является переменными величинами, и могут принимать различные значения в зависимости от количества единиц совокупности, попавших в выборку. Поэтому определяется средняя из возможных ошибок (μ). Величина μ зависит от степени колеблемости значений признака в генеральной совокупности и от численности выборки:

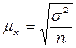
Если выборочное наблюдение применяется для определения доли признака, то средняя ошибка выборки для доли определяется по формуле:

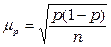
При бесповторном отборе средняя ошибка выборки для количественных признаков равна:

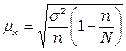
а ошибка выборки для доли равна:

Множитель 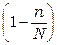всегда меньше единицы, потому что выборочная совокупность не может быть больше генеральной. Поэтому величина средней ошибки выборки при бесповторном отборе меньше, чем при повторном.

Для решения практических задач средней ошибки выборки недостаточно, потому что фактическая ошибка может быть больше или меньше средней ошибки выборки. Поэтому пользуются не средней, а предельной ошибкой выборки, т. е. пределами, за которые не выйдет фактическая ошибка выборки.

Предельная ошибка выборки зависит от того, с какой вероятностью должна гарантироваться ошибка выборки. Уровень вероятности определяется на основе теоремы П. Л.Чебышева (с уточнениями А. М. Ляпунова) при помощи специального коэффициента, обозначаемого буквой "t". Так как возможные ошибки выборки подчиняются закону нормального распределения, то можно утверждать, что в пределах заключается 683 выборочных средних из 1000, т. е. вероятность такого утверждения Р = 0,683; в пределах 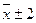- 954 выборочных средних из 1000, т. е. Р = 0, 954 и в пределах 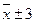- 997 из 1000 или Р = 0,997. Это так называемое правило трёх сигм.

Предельная ошибка выборки равна , где t - коэффициент, зависящий от вероятности, с которой гарантируется ошибка выборки. Она называется ещё коэффициент доверия. При 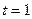вероятность Р = 0,683, при вероятность Р = 0, 954, при 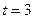вероятность Р = 0,997. Таким образом, зависит от трёх факторов: степени колеблемости явления (σ²); объёма выборки (n) и от необходимой гарантированной вероятности (t).

Рассмотренные формулы μ и применяются при собственно-случайной и механической выборках. При других видах выборки (типической, серийной, комбинированной) формулы средней и предельной ошибок выборки будут другие.

Дата добавления: 2014-01-07