
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интервальный вариационный ряд распределения
|
|
|
|
Каждое значение непрерывного признака как правило имеет частоту встречаемости равную 1, поэтому построение вариационного ряда по типу дискретного ряда здесь невозможно. Для непрерывного признака строится интервальный вариационный ряд. Интервальный вариационный ряд может быть построен также и по дискретному признаку в том случае если он принимает значения в очень широком диапазоне (например число жителей в населенном пункте может изменяться от 1-го до нескольких миллионов). В интервальном вариационном ряду в левой колонке таблицы вместо отдельных значений записываются их интервалы, а в правой – вместо частот для отдельных значений признака записываются частоты интервалов, то есть сколько единиц имеют значения признака в пределах того или иного интервала. Следовательно, макет интервального вариационного ряда выглядит так:
Таблица 2.2.2
Интервальный вариационный ряд распределения …………
| Интервалы значений признака | Частота Частота интервала (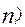
|
| от до | |
| от до | |
| …………… | |
| Итого | Сумма частот (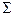 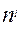 ) )
|
Построение интервального ряда распределения включает в себя несколько этапов.
На первом этапе определяется число интервалов (групп) на которое подразделяется совокупность. Наиболее часто используемыми формулами для определения числа интервалов являются две:  и
и 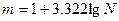 , где
, где  число интервалов. а
число интервалов. а  - общая численность совокупности. Эти формулы дают схожую оценку числа интервалов при общей численности совокупности примерно до 50 единиц. При большей совокупности обнаруживаются большие различия. Например, при N = 100, по первой формуле число интервалов равно 10, а по второй -7, при N =1000 соответственно 32 и 10. и предпочтение следует отдавать второй формуле.
- общая численность совокупности. Эти формулы дают схожую оценку числа интервалов при общей численности совокупности примерно до 50 единиц. При большей совокупности обнаруживаются большие различия. Например, при N = 100, по первой формуле число интервалов равно 10, а по второй -7, при N =1000 соответственно 32 и 10. и предпочтение следует отдавать второй формуле.
Любой интервал содержит нижнюю и верхнюю границы На втором этапе следует рассчитать шаг интервала., то есть разницу между этими границами. Эта разница для всех интервалов должна быть одинаковой. Для расчета шага интервала обычно используется формула: 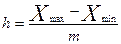 , где
, где 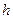 - искомый шаг интервала;
- искомый шаг интервала;  - максимальное в совокупности значение признака;
- максимальное в совокупности значение признака;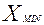 - минимальное в совокупности значение признака;
- минимальное в совокупности значение признака;  число интервалов. Если при изучении ранжированного ряда обнаружится, что максимальное или минимальное (или даже несколько значений) сильно отличаются от остальных, то при расчете шага интервала следует использовать соответственно не максимальное, а предшествующее ему значение, не минимальное, а следующее в ранжированном ряду значение признака. В противном случае может получиться, что в одном- двух интервалах будут сосредоточены все наблюдения.
число интервалов. Если при изучении ранжированного ряда обнаружится, что максимальное или минимальное (или даже несколько значений) сильно отличаются от остальных, то при расчете шага интервала следует использовать соответственно не максимальное, а предшествующее ему значение, не минимальное, а следующее в ранжированном ряду значение признака. В противном случае может получиться, что в одном- двух интервалах будут сосредоточены все наблюдения.
Шаг интервала обычно рассчитывают с той же точностью с какой представлены значения признака в изучаемой совокупности. Иногда шаг интервала берут с точностью на один знак меньше той, какая имеет место в исходной совокупности. Если при расчете шага интервала требуется округление до заданной точности, то округление производят всегда в большую сторону.
После определения шага интервала следует найти границы интервалов: первый интервал в качестве нижней границы имеет 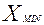 , в качестве верхней
, в качестве верхней 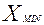 +
+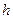 ; второй интервал в качестве нижней имеет верхнюю границу первого интервала,то есть
; второй интервал в качестве нижней имеет верхнюю границу первого интервала,то есть 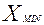 +
+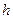 , для получения верхней границы этого интервала надо вновь прибавить шаг интервала, то есть
, для получения верхней границы этого интервала надо вновь прибавить шаг интервала, то есть 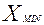 +
+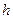 ,+
,+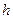 =
=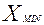 + 2
+ 2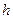 и так далее. Если при определении шага интервала пришлось отказаться от
и так далее. Если при определении шага интервала пришлось отказаться от 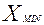 , то в первом интервале сразу находится верхняя граница, для чего к значению, которое использовалось при расчете шага интервала следует прибавить шаг интервала, нижняя граница первого интервала не обозначается. Сам интервал будет открыт снизу. Если при расчете шага интервала пришлось отказаться от максимального значения, для того, чтобы и это значение присутствовало в интервальном ряду, открытым сверху делают последний интервал. Определив границы интервалов, далее следует подсчитать сколько единиц попало в каждый интервал. Для этого удобнее всего воспользоваться ранжированным рядом, обозначив на нем границы интервалов. Если единица имеет значение признака на границе интервала, то она может вой- ти только в один интервал; в какой именно решает сам исследователь – в нижний (принцип включительно) или верхний (принцип исключительно). Результаты подсчетов оформляются в таблице, представленной ранее на макете. Графически интервальный вариационный ряд отображается в виде гистограммы распределения, при этом на оси абсцисс откладываются интервалы, а на оси ординат - частоты интервалов Вид такого графика следующий
, то в первом интервале сразу находится верхняя граница, для чего к значению, которое использовалось при расчете шага интервала следует прибавить шаг интервала, нижняя граница первого интервала не обозначается. Сам интервал будет открыт снизу. Если при расчете шага интервала пришлось отказаться от максимального значения, для того, чтобы и это значение присутствовало в интервальном ряду, открытым сверху делают последний интервал. Определив границы интервалов, далее следует подсчитать сколько единиц попало в каждый интервал. Для этого удобнее всего воспользоваться ранжированным рядом, обозначив на нем границы интервалов. Если единица имеет значение признака на границе интервала, то она может вой- ти только в один интервал; в какой именно решает сам исследователь – в нижний (принцип включительно) или верхний (принцип исключительно). Результаты подсчетов оформляются в таблице, представленной ранее на макете. Графически интервальный вариационный ряд отображается в виде гистограммы распределения, при этом на оси абсцисс откладываются интервалы, а на оси ординат - частоты интервалов Вид такого графика следующий

|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1980; Нарушение авторских прав?; Мы поможем в написании вашей работы!