Закон сложения ( разложения ) вариации

Модульная единица 2. Закон сложения (разложения вариации)

Резюме

Построение рядов распределения с последующей их количественной характеристикой позволило дать всестороннюю оценку изучаемой совокупности: установить типичный и наиболее часто встречающийся размер признака, установить типичный размер колеблемости, форму распределения.

Цель и задачи изучения модульной единицы состоят в освоении центрального в статистике закона – сложения и разложения вариации. Знание этого закона необходимо при изучении последующих разделов курса

Если совокупность, состоящую из N единиц разбить на m групп, численностью по 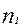единиц, то общий объем вариации будет представлять собой сумму вариации межгрупповой и внутригрупповой, то есть 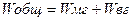. Для раскрытия содержания каждого из названных объемов вариации введем следующие обозначения: - значение признака по каждой единице наблюдения, при этом индекс i означает принадлежность к соответствующей группе i (1, 2, 3 ……m), а индекc j - номер наблюдения в группе. Символом 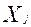= 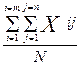обозначим общую среднюю по совокупности, символом 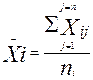- среднее значение признака по каждой из групп. Тогда общий объем вариации признака будет равен: 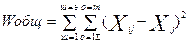, то есть для его нахождения надо каждое значение признака сравнить с общей средней, полученные разности возвести в квадрат, а затем квадраты суммировать. Для получения вариации межгрупповой необходимо с общей средней сравнивать средние групповые, средней групповой мы как бы замещаем каждое из значений входящее в соответствующую группу:

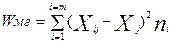
Вариация внутригрупповая складывается из вариации внутри каждой из групп: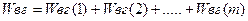

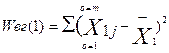В свою очередь для нахождения вариации внутри каждой группы, надо каждое значение входящее в эту группу сравнить со средней по этой группе, полученные разности возвести в квадрат и квадраты суммировать. Например, для первой группы для группы m 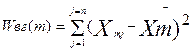. Таким образом, закон разложения вариации в целом будет иметь вид:

= + +….+

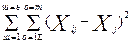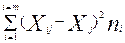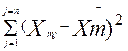
Примем это равенство без доказательства, но в последующем проверим его на числовом примере.

Дата добавления: 2014-01-07