Два типа задач решаемых на основе выборочного метода

Модульная единица 3 Типовые задачи решаемые на основе выборочного метода

Резюме по модульной единице 2

Вопросы для повторения

6-1.Какова природа конкретной, средней и предельной ошибок?

6-2.Как соблюсти принцип равновероятности каждой единицы попасть в выборку при выборочном устном опросе студентов?

6-3 Каков источник систематической ошибки?

6-4.Какова вероятность появления ошибки в 2.5 раза превышающей среднюю?

6-5.Какие различия в знаках (+, -) имеют систематические и случайные ошибки?

6-6.Каковы основные пути уменьшения средней и предельной ошибки?

6-7.При какой выборочной доле имеет место ее наибольшая ошибка?

6-8.При какой доле признака имеет место ее наименьшая ошибка 7

6-9.При каких выборках (больших или малых) при прочих равных условиях имеет место большая предельная ошибка?

Использование выборочного метода неизбежно сопряжено с появлением ошибок. Случайный характер этих ошибок, нормальный или t - Стьюдента закон их распределения позволяет определить их средний и предельный размер и видеть пути их снижения

Выборочный метод используется для решения двух типов задач. Первый тип задач так или иначе связан с получением оценок параметров генеральной совокупности, а второй состоит в проверке на основе выборки некоторого предположения относительно генеральной совокупности. Первый тип и включает в себя три задачи: 1) установление границ, в которых с принятым доверительным уровнем вероятности находится параметр генеральной совокупности; 2) расчет минимально необходимой численности выборки, обеспечивающей появление ошибки не больше заданной; 3) определение уровня вероятности появления заданной ошибки при ограниченной численности выборки. Рассмотрим последовательность решения каждой из перечисленных задач на примере использования выборочного метода для оценки генеральной средней и доли

3.2 Интервальная оценка генеральной средней и доли. Данная задача решается в такой последовательности: 1) из генеральной совокупности осуществляется выборка численностью 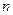единиц; 2) по выборочной совокупности определяется выборочная средняя, как оценка для средней генеральной; при ее расчете может быть использована формула средней арифметической простой 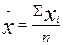или (если выборочные данные представлены вариационным рядом распределения) средней арифметической взвешенной ; 3) по выборочной совокупности определяется значение выборочного среднего квадратического отклонения по формулам: 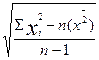(для случая простой средней) или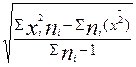

(для случая, когда выборочная средняя определяется как средняя взвешенная); 4) определяется средняя ошибка выборочной средней 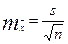; 5) устанавливается доверительный уровень вероятности (Р); 6) для принятого доверительного уровня вероятности по соответствующим таблицам находят значение коэффициента t; 7) определяются границы предельной ошибки ; 8) с принятым доверительным уровнем вероятности генеральная средняя находится в интервале 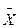0 = ±;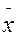

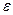Для интервальной оценки генеральной доли из генеральной совокупности формируется выборка численностью 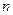единиц, затем по выборке определяется число единиц (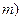с неким качеством. Соотношение 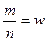- это оценка доли в генеральной совокупности, ее средняя ошибка будет равна 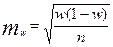. Для нахождения границ предельной ошибки для доли следует выбрать доверительный уровень вероятности- Р, по таблицам интеграла вероятностей нормального распределения (доля обычно оценивается на основе больших выборок) найти коэффициент t и, следовательно, границы предельной ошибки для доли составят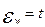 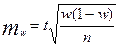. Определив возможные границы предельной ошибки можно установить с заданным уровнем вероятности границы доли признака в генеральной совокупности W =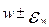

Дата добавления: 2014-01-07