
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопросы для повторения. Установив соответствие фактического распределения ожидаемому, можно прогнозировать ожидаемые численности по группам
|
|
|
|
Резюме
Установив соответствие фактического распределения ожидаемому, можно прогнозировать ожидаемые численности по группам, интервалам, исходя из общей численности совокупности
Модульная единица 2 - как критерий независимости
как критерий независимости
Цель изучения данной модульной единицы - освоить еще один аспект использования критерия  , который имеет весьма широкое применение при обработке экспериментальных данных, когда эти данные носят характер распределения численностей (растений, животных, земельных участков) и предназначены для установления наличия или отсутствия взаимосвязи между признаками.
, который имеет весьма широкое применение при обработке экспериментальных данных, когда эти данные носят характер распределения численностей (растений, животных, земельных участков) и предназначены для установления наличия или отсутствия взаимосвязи между признаками.
 в качестве критерия независимости используется в том случае, если выборочная совокупность распределена одновременно по 2- м признакам и необходимо установить зависит ли распределение по одному признаку от распределения по другому. Выборочные данные в этом случае могут быть представлены в виде такой, например, таблицы с двумя входами, где по первому признаку выделено три группы интервала k=3, а по второму четыре l=4:
в качестве критерия независимости используется в том случае, если выборочная совокупность распределена одновременно по 2- м признакам и необходимо установить зависит ли распределение по одному признаку от распределения по другому. Выборочные данные в этом случае могут быть представлены в виде такой, например, таблицы с двумя входами, где по первому признаку выделено три группы интервала k=3, а по второму четыре l=4:
| Группы (интервалы по первому признаку | Группы (интервалы) по второму признаку | Итого по строкам | |||
| а | В | с | d | ||
| А | 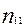
| … | … | … | 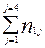
|
| В | … | … | … | … | 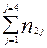
|
| С | … | … | ... | 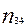
| 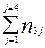
|
| Итого по столбцам | 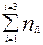
| 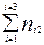
| 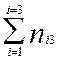
| 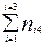
| 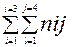 =n =n
|
В качестве нулевой гипотезы выдвигается предположение, что распределение по первому признаку не зависит от распределения по второму. Такая постановка нулевой гипотезы определяется во-первых тем, что этой гипотезе принадлежит абсолютное большинство возможных значений критерия, а во-вторых исследователь, как правило верит в то, что эта зависимость имеет место, поэтому в качестве нулевой гипотезы выдвигается противоположное предположение. Альтернативной гипотезой будет предположение о наличии взаимосвязи между распределениями С практической точки зрения справедливость нулевой гипотезы означает отсутствие взаимосвязи между признаками, справедливость альтернативной – наличие такой взаимосвязи в генеральной совокупности.
В качестве критерия воспользуемся критерием  , при этом надо предварительно подтвердить отсутствие внутри групп взаимосвязи между наблюдениями. Фактическое значение критерия
, при этом надо предварительно подтвердить отсутствие внутри групп взаимосвязи между наблюдениями. Фактическое значение критерия  при использовании его в качестве критерия независимости определяется по той же формуле, что и аспекте согласия, при этом, поскольку распределение имеет место 2- м признакам формула несколько усложняется, то есть отношения
при использовании его в качестве критерия независимости определяется по той же формуле, что и аспекте согласия, при этом, поскольку распределение имеет место 2- м признакам формула несколько усложняется, то есть отношения 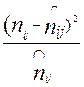 должны быть просуммированы вначале по строкам, а затем по столбцам (или наоборот), то есть
должны быть просуммированы вначале по строкам, а затем по столбцам (или наоборот), то есть 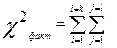
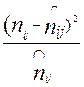
Ожидаемые частоты должны соответствовать нулевой гипотезе о независимости распределений; математически это означает, что распределение единиц по столбцам внутри каждой строки должно таким же, как по столбцам распределяется вся совокупность и соответственно распределение единиц по строкам внутри каждого столбца должно быть таким каково распределение единиц по строкам в целом по совокупности. Этот принцип реализуется в формуле 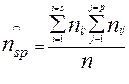 , то есть для нахождения ожидаемой частоты с координатами: строка s и столбец p надо обратиться к фактическим частотам, найти произведение итога по строке s на итог по столбцу р и полученное произведение разделить на общую численность совокупности. Действительно, эта формула адекватна выше указанному принципу поскольку отношение
, то есть для нахождения ожидаемой частоты с координатами: строка s и столбец p надо обратиться к фактическим частотам, найти произведение итога по строке s на итог по столбцу р и полученное произведение разделить на общую численность совокупности. Действительно, эта формула адекватна выше указанному принципу поскольку отношение  - это доля строки s в общей численности совокупности и эту долю мы распространяем на
- это доля строки s в общей численности совокупности и эту долю мы распространяем на  то есть на столбец p. Отношение
то есть на столбец p. Отношение 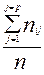 есть доля столбца р в общей численности совокупности и эту долю мы распространяем на строку s.
есть доля столбца р в общей численности совокупности и эту долю мы распространяем на строку s.
При определении ожидаемых частот естественно следует производить округление до целых значений. Правильность расчета ожидаемых частот проверяется сравнением итогов по строкам и столбцам для фактических и ожидаемых частот. Эти итоги должны совпадать (за счет округления могут иметь место несовпадения в несколько единиц). Численность каждой ожидаемой частоты должна превышать 5 единиц, в противном случае прежде чем рассчитывать фактическое значение критерия следует произвести объединение интервалов.
В заключение найденное фактическое значение критерия ( факт) следует сравнить с табличным (
факт) следует сравнить с табличным ( табл), при этом табличное значение зависит от установленного уровня значимости и от числа степеней свободы, которое в данном аспекте использования критерия
табл), при этом табличное значение зависит от установленного уровня значимости и от числа степеней свободы, которое в данном аспекте использования критерия  рассчитывается по формуле df (
рассчитывается по формуле df (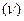 = (k-1)(l=1), где к и l -соответственночисло строк и столбцов. В зависимости от соотношения
= (k-1)(l=1), где к и l -соответственночисло строк и столбцов. В зависимости от соотношения  факт и
факт и  табл принимается соответственно или нулевая или альтернативная гипотезы.
табл принимается соответственно или нулевая или альтернативная гипотезы.
11-1. В каком случае критерий используется как критерий независимости?
используется как критерий независимости?
11-2. Какая гипотеза выступает в качестве нулевой при использовании критерия  в аспекте независимости? Почему?
в аспекте независимости? Почему?
11-3.Какой алгоритм расчета фактического значения критерия  используется при использовании его в качестве критерия независимости?
используется при использовании его в качестве критерия независимости?
11-4. Какие практические выводы следуют при принятии нулевой и альтернативной гипотез?
11-5. Какой математический принцип используется для нахождения ожидаемых частот?
11-6. Каков алгоритм расчета ожидаемых частот?
11-7. Как проверить правильность расчета ожидаемых частот?
11-8. Как установить число степеней свободы при использовании критерия  как критерия независимости?
как критерия независимости?
|
|
|
Дата добавления: 2014-01-07; Просмотров: 301; Нарушение авторских прав?; Мы поможем в написании вашей работы!