Лекция 6. Последний из рассматриваемых аспектов использования критерия позволяет сделать вывод , что в совокупности с ранее рассматриваемыми аспектами применение

Резюме

Последний из рассматриваемых аспектов использования критерия позволяет сделать вывод, что в совокупности с ранее рассматриваемыми аспектами применение изучаемого критерия позволяет использовать выборочные совокупности для всесторонней проверки генеральных совокупностей на предмет схожести их структур, соответствия распределения теоретическому, наличия взаимосвязей

Тестовые задания к лекции

ТЕСТ 5-1

Какие из названных критериев используются при проверке гипотез относительно распределения численностей

1. Критерий t - Стьюдент

2. Критерий F- Фишера

3. Критерий Госсета

4. Критерий Тьюки

5. - Пирсона

ТЕСТ 5- 2

Если требуется проверить гипотезу о соответствии фактического распределения нормальному, то в каком аспекте используется в этом случае критерий - Пирсона?

1. Как критерий согласия

2. Как критерий независимости

3. Как критерий однородности

ТЕСТ 5-3

Если требуется установить по данным выборочного распределения взаимосвязаны ли специализация предприятий и степень их убыточности, то в каком аспекте используется критерий - Пирсона?

1. Как критерий согласия

2. Как критерий независимости

3. Как критерий однородности

ТЕСТ 5-4

Если требуется установить на основе двух выборок одинаков ли состав

полей по степени их засоренности, то критерий - Пирсона исполься как критерий …..

1……однородности

2…….независимости

3…….однородности

ТЕСТ 5-5

В формуле для расчета фактического значения критерия - Пирсона:

= , что представляют собой ?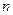

1. Фактические численности по группам (интервалам) выборки

2. Ожидаемые численности по группам (интервалам)

3. Долю каждого интервала в общей численности выборки

ТЕСТ 5- 6

В формуле для расчета фактического значения критерия - Пирсона = , что представляют собой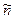

1. Фактические численности по группам (интервалам) выборки

2. Ожидаемые численности по группам (интервалам

3. Долю каждого интервала в общей численности выборки

ТЕСТ 5-7

В чем может состоять источник (причина) разности ?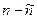

1. В ошибке расчета ожидаемых часто

2. В игре случая

3. В существенном отличии фактического распределения от ожидаемого

ТЕСТ 5-8

В чем смысл ожидаемых частот (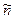) при использовании критерия - Пирсона в качестве критерия согласия

1. Так распределялась бы выборочная совокупность в соответствии с нулевой гипотезой

2. Так распределялась бы выборка при соответствии фактического

распределения ожидаемо

3. Это некоторое стандартное распределение, которое должно присутствовать в любом случае

ТЕСТ 5-9

Как проверить правильность расчета ожидаемых частот

1. Провести расчеты повторно

2. Сравнить на отличие от 0 (нуля) суммы фактических и ожидаемых частот

3.Сравнить на отличие от 0 (нуля)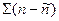

ТЕСТ 5-10

В чем смысл ожидаемых частот при использовании критерия - Пирсона как критерия независимости?

1. Такие частоты должны иметь место при независимости распределений по двум признакам

2. Такие частоты должны иметь место при справедливости нулевой гипотезы

3.Это некий постоянный стандарт с каким должны сравниваться все распределения по 2- м признакам.

ТЕСТ 5-11

На основе какого принципа находятся (рассчитываются) ожидаемые частоты при проверке гипотезы о независимости распределений?

1. Внутри каждой группы. выделенной по первому признаку, распределение по второму признаку должно быть одним и тем же

2. Внутри каждой группы, выделенной по второму признаку, распределение по первому должно быть таким как и в целом по совокупности

3. Внутри каждой группы, выделенной по второму признаку распределение единиц по первому признаку должно быть одним и тем же

ТЕСТ 5-12

Как проверить правильность расчета ожидаемых частот при использовании критерия - Пирсона в качестве критерия независимости

1.Повторным расчетом

2. Сравнением сумм фактических и ожидаемых частот по столбцам и строкам таблиц распределения по 2- м признакам

3.Сравнением общей численности фактических и ожидаемых частот.

ТЕСТ 5-13

Если в каком –либо интервале (группе) его частота оказалось менее

5 единиц, каковы будут последующие действия?

1. Исключить данную группу из последующих расчетов

2. Объединить данный интервал с соседним и независимо от численности объединенного интервала продолжить расчеты

3. Осуществлять объединение до тех пор, пока в объединенном интервале будет не менее 5 единиц

4. Проигнорировав этот факт, продолжать расчеты

ТЕСТ 5-14

От чего зависит табличное значение критерия - Пирсона?

1. От численности выборки (выборок)

2.От числа выделенных групп (интервалов)

3.От числа степеней свободы

4.От уровня значимости

ТЕСТ 5-15

При каком из аспектов использования критерия - Пирсона в алгоритме расчета фактического значении критерия отсутствуют ожидаемые частоты?

1. Как критерий согласия

2. Как критерий однородности

3. Как критерий независимости

ТЕСТ 5-16

Что играет решающую роль в формуле для определении фактического

значения критерия - Пирсона при его использовании в качестве критерия однородности?

1. Численность первой выборки

2. Численность второй выборк

3. Разница в долях по каждой группе

Дата добавления: 2014-01-07