
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Модуль 2 Модульная единица 15
|
|
|
|
Проверка гипотезы относительно доли признака. Проверка гипотезы о принадлежности резко выделяющегося значения признака изучаемой совокупности
Занятие 12
Задача 1 Проверка гипотезы относительно доли признака
Условия: имеется генеральная совокупность, в которой единицы характеризуются неким качественным признаком, имеющим альтернативный характер.
Требуется: на основе большой выборки установить равна ли в генеральной совокупности доля единиц с определенным качеством величине Q
Решение:
1.1) из генеральной совокупности произведем механическим способом выборку численностью n единиц; подсчитаем число единиц в выборке с определенным качеством (m); найдем выборочную долю этих единиц 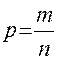
1.1) выдвинем две гипотезы Н9: Р=Q и альтернативная Р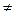 Q;
Q;
1.2) определимся с уровнем значимости;
1.3) поскольку выборки большие, для проверки выдвинутых гипотез воспользуемся критерием t – нормального распределения;
1.4) рассчитаем фактическое значение критерия по формуле  , где p – доля единиц определенного качества по выборке, g - доля единиц противоположного качества по выборке; n – численность выборки;
, где p – доля единиц определенного качества по выборке, g - доля единиц противоположного качества по выборке; n – численность выборки;
1.5) сравним фактическое значение критерия с табличным, которое зависит только от уровня значимости и сделаем соответствующий вывод.
Задача 2 Проверка гипотезы относительно доли признака в двух генеральных совокупностях
Условие: имеются две генеральных совокупности, в которых единицы характеризуются неким качественным признаком, имеющим альтернативный характер.
Требуется: установить равны или нет в двух генеральных совокупностях доли единиц одинакового качества
Решение:
2.1) из каждой генеральной совокупности произведем выборки численностью 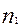 и
и 
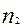 единиц;
единиц;
2.2) по каждой выборке установим число единиц определенного качества:(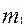 и
и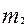 );
);
2.3) по каждой выборке найдем долю единиц определенного качества:
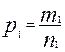 и
и  ;
;
2.4) выдвинем гипотезы: нулевую о равенстве долей в двух генеральных совокупностях,  то есть
то есть  :
:  .и альтернативную - ненаправленную
.и альтернативную - ненаправленную 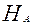 :
:  или направленную -
или направленную - 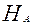 :
:  (
(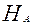 :
: 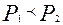 );
);
2.5) определимся с уровнем значимости;
2.6) в качестве критерия для проверки выдвинутых гипотез используется критерий t - нормального распределения;
2.7) расчет фактического значения критерия может производится по двум алгоритмам: если каждая из выборочных доли ( ) лежит в интервале
) лежит в интервале 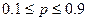 , то формула для расчета фактического значения критерия будет следующей
, то формула для расчета фактического значения критерия будет следующей 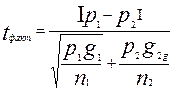 , где
, где 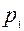 - доля единиц с определенным качеством по первой выборке;
- доля единиц с определенным качеством по первой выборке;  - доля таких единиц по второй выборке;
- доля таких единиц по второй выборке; 
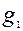 ,
,  - доля единиц с противоположным качест-
- доля единиц с противоположным качест-
вом соответственно по первой и второй выборкам; 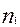
 и
и 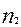 численности выборок.
численности выборок.
Если же хотя бы одна из выборочных долей лежит вне указанного выше интервала, то для расчета фактического значения критерия требуется предварительное 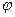 (фи) преобразование выборочных долей, при этом значения
(фи) преобразование выборочных долей, при этом значения  находятся по специальным таблицам. Фактическое значение критерия t –нормального распределения находят по формуле:
находятся по специальным таблицам. Фактическое значение критерия t –нормального распределения находят по формуле:
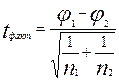 , где
, где  и
и  - преобразованные значения выборочных
- преобразованные значения выборочных
долей.
2.8) по таблицам находим критическое значение критерия; сравнивая его фактическое значение с табличным формулируем вывод относительно выдвинутых гипотез
Задача 3 Проверка гипотезы о принадлежности резко выделяющегося значения признака изучаемой совокупности
Условие: имеется выборочная совокупность.
Требуется: установить принадлежат ли максимальное и минимальное значение признака исследуемой совокупности.
|
|
|
Дата добавления: 2014-01-07; Просмотров: 365; Нарушение авторских прав?; Мы поможем в написании вашей работы!