Решение. Модуль3. Модульные единицы 18, 19

Модуль3. Модульные единицы 18, 19

Занятие 17 Оценка выборочных показателей связи

Условие: имеется уравнение связи полученное по выборочным данным (см занятие 15).

Требуется: оценить полученные по выборке показатели связи.

1.1) во- первых следует проверить гипотезу о существенности уравнения в целом. Эта гипотеза проверяется на основе критерия F – Фишера, фактическое значение которого определяется как отношение 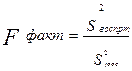Для нахождения необходимых дисперсий соответствующие объемы вариаци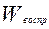и (и 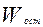) следует разделить на их число степеней свободы , где m- число параметров уравнения; , где n- число наблюдений на основе которых построено уравнение связи. Полученное фактическое значение критерия сравнивается с табличным (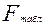), которое зависит от уровня значимости и числа степеней свободы воспроизведенной и остаточной вариации. Если 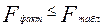принимается гипотеза о несущественности уравнения и дальнейшая оценка показателей связи не требуется, если же принимается гипотеза о существенности уравнения и требуется дальнейшая оценка показателей связи. Расчет фактического значения критерия F произведем используя стандартную программу «Регрессия» EXCEL. В выходной таблице этой программы даны также степени свободы, необходимые для определения табличного значения критерия

1.2) проверим гипотезу относительно выборочного коэффициента регрессии. для чего вначале выдвинем гипотезы нулевую в генеральной совокупности коэффициент регрессии В=0 и альтернативную - в генеральной совокупности этот коэффициенты нулю не равен (В≠0).

1.3) определимся с уровнем значимости;

1.4) поскольку при построении уравнения была использована малая выборка, то проверку гипотезы относительно коэффициента регрессии проведем с использованием критерия t-Стьюдента.

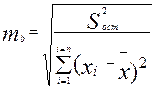Фактическое значение данного критерия найдем по формуле , где - выборочный коэффициент регрессии. - средняя ошибка коэффициента регрессии, которая рассчитываем по формуле , где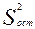- остаточная вариация результативного признака; - объем вариации факторного признака.

Остаточную вариацию результативного признака находим на основе выходной таблицы программы «Регрессия «EXCEL Объем вариации факторного признака на основе программы «Описательная статистика«

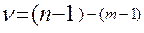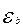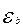
1.5) фактическое значение критерия сравниваются с табличным, которое кроме уровня значимости зависит от числа степеней свободы, которое равно , где n –число наблюдений, m- число параметров уравнения. По результатам сравнения формулируем соответствующий вывод. Если была принята альтернативная гипотеза, то находим границы коэффициента регрессии в генеральной совокупности: В = b ±, где - предельная ошибка коэффициента регрессии, определяемая по формуле

1.6) проверим гипотезу относительно коэффициента корреляции. Для чего вначале выдвинем гипотезы: нулевую R=0 и альтернативную - в генеральной совокупности эти коэффициент корреляции R≠ 0.

Определимся с уровнем значимости.

В качестве критерия надо воспользоваться критерием t – Стьюдента, поскольку выборка малая.

Фактическое значение критерия рассчитаем по формул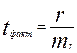е , где

, при этом r- выборочный коэффициент корреляции

Фактическое значение критерия сравниваются с табличным, которое кроме уровня значимости зависит от числа степеней свободы, которое равно 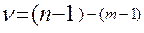, где n –число наблюдений, m- число параметров уравнения. По результатам сравнения формулируем соответствующий вывод.

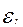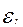Если была принята альтернативная гипотеза о существенности коэффициента корреляции следует найти его границы в генеральной совокупности R= r ±, где - предельная ошибка коэффициента корреляции равная

ГЛОССАРИЙ УМК дисциплины «МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»

Термин	Содержание термина
Вариация	Изменчивость, колеблемость признака по единицам совокупности
- вариации объем	Общая колеблемость признака, определяемая как сумма квадратов отклонений отдельных значений признака от средней арифметической
-вариации размах	Разность между максимальным и минимальным значениями признака
Гипотеза	Предположение
-статистическая	Предположение о законе распределения или параметре генеральной совокупности. Статистические гипотезы выдвигаются, как правило, в паре: нулевая и противоположная ей альтернативная. Одна из этих гипотез принимается в ходе проверки на основе выборки
Гистограмма	Графическое отображение интервального вариационного ряда распределения
Граница	Черта, означающая изменение качества
- доверительная	Интервал в каком с неким уровнем вероятности на основе выборки устанавливается значение параметра генеральной совокупности
Дисперсия	Один из показателей вариации, представляет собой объем вариации, приходящийся на единицу совокупности
Корреляция	Особый тип связи между признаками, когда следствие неоднозначно меняется по воздействием причины
Коэффициент	Отношение
- вариации	Отношение стандартного отклонения к средней арифметической, выраженное в %. Показывает среднее процентное отклонение значений признака от средней арифметической
- детерминации	Показатель тесноты при корреляционной связи. Представляет собой отношение воспроизведенной (связанной с действием фактора) вариации к общей вариации
- корреляции	Показатель тесноты связи. представляет собой производную (корень квадратный) величину от коэффициента детерминации
- отдельного определения	Один из показателей тесноты связи. Показывает вклад каждого фактора в коэффициент множественной детерминации
- регресии	Один из коэффициентов в уравнении корреляционной связи; при линейном ее характере показывает среднее изменение результативного признака при изменении фактора на 1
Критерий	Инструмент для проверки статистических гипотез. Представляет собой случайную величину со своим законом распределения
Медиана	Значение признака делящее ранжированный ряд на две равные части по численности
Мода	Значение признака с наибольшей частотой встречаемости
НСР	Наибольшая случайная разность- максимальные различия между количественными характеристиками выборок, произведенных из одной и той же генеральной совокупности
Область	Территория
- согласия	Совокупность значений критерия, при которых принимается нулевая гипотеза
- критическая	Совокупность значений критерия, при которых принимается альтернативная гипотеза
Огива	Графическое отображение ранжированного ряда распределения
Отклонение	Отличие от чего- то
- среднее линейное	Один из показателей вариации представляет собой среднее из отклонений каждого значения признака от средней арифметической, взятых по абсолютной величине
-стандартное (среднее квадратическое)	Один из показателей вариации Показывает насколько в среднем каждое значение признака отличается от средней арифметической. рассчитывается как корень квадратный из дисперсии
Оценка	Статистическая характеристика выборочной совокупности, на основе которой делается суждение о соответствующем параметре генеральной совокупности
Ошибка	Заблуждение, неточность
- выборки	Разница между оценкой и оцениваемым параметром генеральной совокупности. Различают среднюю и предельную ошибку выборки
- первого и второго рода	Возможные ошибки при проверке статистических гипотез
Полигон	Графическое отображение вариационного ряда распределения дискретного признака
Признак	Одно из свойство единиц, образующих совокупность
Ряд	Расположение чего-то в некоторой последовательности
- ранжированный	Расположение единиц совокупности в порядке возрастания или убывания значения признака
- вариационный	Упорядочение статистической совокупности путем обозначения значений признака и частоты встречаемости этих значений
Совокупность статистическая	Собрание единиц, объединенных неким общим для всех их свойством (определяющим свойством)
- генеральная	Совокупность всех без исключения единиц с общим для всех свойством
- выборочная	Специально отобранная часть генеральной совокупности, предназначенная для моделирования генеральной совокупности
Средняя	Некий типичный для совокупности размер признака. Вид средней определяется особенностями признака, по которому она рассчитывается.
Степень свободы	Число единиц в совокупности, имеющих возможность изменять свою величину, если по совокупности найдена количественная характеристика. Степени свободы используются для нахождения оценок и табличных значений критерия
Частота	Число, показывающее сколько единиц имеют одно и то же значение признака
Уровень	Некое достижение, граница
-значимости	Вероятность допущения ошибки при проверке статистической гипотезы
-доверия	Вероятность достоверности полученных статистических выводов

ТЕСТОВЫЕ ЗАДАНИЯ ИТОГОВОГО КОНТРОЛЯ

Дата добавления: 2014-01-07