
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Абсолютные показатели вариации
|
|
|
|
.
Таким образом, в течение года ежеквартально стоимость основных фондов предприятия в среднем возрастала на 3,1%.
Осреднение относительных показателей интенсивности (ОПИ) всегда осуществляется по взвешенным формулам – арифметическим или гармоническим:
 , где
, где 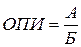 .
.
Пример 6.8. Плотность населения трех регионов в составе одного субъекта федеративного государства составляет 10, 12 и 15 тыс. чел./км2 при численности населения 2,5; 3,2; 4,5 млн. чел. соответственно (цифры условные). Рассчитаем плотность населения субъекта государства на основе значений этого показателя для отдельных его регионов.
Решение.
Обозначим: А – численность населения; Б – площадь территории, на которой оно проживает. Тогда плотность населения рассчитывается по формуле относительного показателя интенсивности:
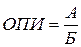 .
.
Учитывая исходные данные, осредним отдельные варианты плотности населения по формуле средней гармонической взвешенной:
 тыс. чел./км2.
тыс. чел./км2.
Все рассмотренные в подразделе 6.2 средние показатели относятся к средним степенным. Помимо них к средним статистическим показателям принято относить показатели структуры статистического ряда распределения (см. подраздел 4.2). Однако их величина не зависит от каждого из осредняемых значений, а определяется структурой ряда распределения.
Лекция 4 СТАТИСТИЧЕСКИЙ АНАЛИЗ ВАРИАЦИИ
Для оценки и сравнения вариации значений количественных признаков рассчитывают статистические показатели вариации. При этом различают абсолютные и относительные показатели вариации.
К абсолютным показателям вариации относят:
· размах вариации
 ;
;
· среднее линейное отклонение (простое и взвешенное)
 ;
;
 ;
;
· дисперсию (простую и взвешенную)
 ;
;
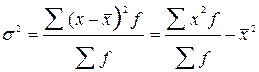 ;
;
· среднеквадратичное отклонение
 .
.
Если значения исследуемого признака не сгруппированы по вариантам, то показатели вариации рассчитывают по формулам простым, в противном случае – по формулам взвешенным (также как и среднее значение показателя). При этом дисперсию можно рассчитать двумя способами – осредняя квадраты отклонений значений признака от среднего значения и осредняя квадраты значений признака с последующим вычитанием из полученного результата квадрата среднего значения.
Очевидно, что при полном отсутствии вариации (все значения признака равны) все рассмотренные показатели равны нулю. По мере усиления вариации их значения увеличиваются.
Пример 7.1. В таблице 7.1 представлены данные о распределении нефтяных скважин нефтяного месторождения по их глубине.
Таблица 7.1
| Глубина скважины, м | 50 - 100 | 100 - 150 | 150 - 200 | 200 - 250 | Итого |
| Число скважин |
Рассчитаем среднюю глубину скважин месторождения и все абсолютные показатели вариации глубины скважин.
Решение.
Обозначим: х – середины интервалов глубины скважин; ƒ – число скважин, попавших в заданный интервал.
Имеет место группировка значений статистического признака по интервалам, поэтому расчет искомых показателей необходимо проводить по формулам взвешенным.
Итерационная часть расчета представлена в таблице 7.2. Подставим рассчитанные в этой таблице в используемые ниже формулы.
Размах вариации глубины скважин
 м.
м.
Среднее линейное отклонение
 =
=  = 43,75 м;
= 43,75 м;
Таблица 7.2

| 
| 
| 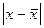
| 
| 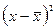
| 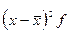
|
| 81,25 | 812,5 | 6601,56 | 66015,6 | |||
| 31,25 | 937,5 | 976,56 | 29296,8 | |||
| 18,75 | 375,0 | 351,56 | 7031,2 | |||
| 68,75 | 1375,0 | 4726,56 | 94531,2 | |||
| Итого | -- | 3500,0 | -- | 196874,8 |
Дисперсия
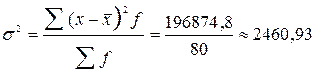 м2.
м2.
Среднеквадратичное отклонение
 м.
м.
Если варианты исследуемого признака заданы интервалами равной ширины, то дисперсию проще рассчитать способом отсчёта от условного нуля по формуле
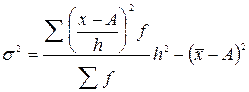 ,
,
где:
h – ширина интервалов;
А – середина интервала с максимальной частотой (условный нуль).
В качестве примера пересчитаем дисперсию глубины скважин нефтяного месторождения способом отсчета от условного нуля, используя исходные данные, представленные в таблице 7.1. В данном случае h = 50 м, A =125 м.
Итерационную часть расчета среднего значения глубины скважин и ее дисперсии отразим в таблице 7.3.
Таблица 7.3

| 
| 
| 
| 
| 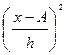
| 
|
| -50 | -1 | |||||
| -1 | ||||||
| Итого | --- | --- | --- |
Согласно данным таблицы 7.3 среднее значение глубины скважин
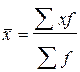 =
= =156,25 м;
=156,25 м;
Дисперсия глубины скважин
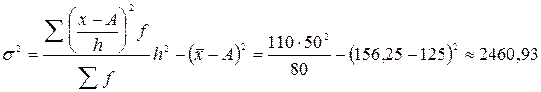 м2.
м2.
Как видно из решения задачи, несмотря на громоздкость формулы, способ отсчета от уловного нуля упрощает расчет дисперсии. И чем больше число интервалов изучаемого признака, тем сильнее будет заметно это упрощение. Причина – в том, что строка расчетной таблицы, соответствующая интервалу с уловным нулем, начиная с четвертой графы, обязательно заполняется нулями, а расчет остальных строк значительно упрощается из-за неизбежного перехода к целым числам, начиная с пятой графы таблицы.
Рассмотренные абсолютные показатели вариации рассчитывают для количественного признака. Они позволяют оценить вариацию признака в абсолютном выражении, но не позволяют сравнить вариацию разных признаков или одного и того же признака, но для разных статистических совокупностей. Для этого необходим переход к относительным показателям вариации, которые будут рассмотрены в подразделе 7.3. Кроме того, на практике часто возникает необходимость оценить вариацию значений альтернативного атрибутивного признака. В этом случае рассчитывают показатель вариации – дисперсию доли. При этом вместо средней величины, характеризующей значения количественного признака, определяют долю одного из значений альтернативного атрибутивного признака
 ,
,
где:
m – число единиц статистической совокупности с одним из двух значений признака;
n – общее число единиц статистической совокупности.
На основе значения доли рассчитывают дисперсию доли, используя формулу
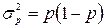 .
.
Как видно из формулы, на оценку вариации не влияет, какое из двух значений признака будет взято в качестве основного (от перемены места множителей произведение не меняется).
При полном отсутствии вариации, когда наблюдается только одно из альтернативных значений, дисперсия доли принимает нулевое значение. По мере усиления вариации ее значение растет и достигает своего максимума 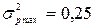 при
при  , то есть когда статистическая совокупность делится по значению альтернативного признака на две равновеликие группы.
, то есть когда статистическая совокупность делится по значению альтернативного признака на две равновеликие группы.
В отличии от абсолютных показателей вариации количественного признака дисперсия доли позволяет сравнивать вариацию разных альтернативных атрибутивных признаков.
Пример 7.2. В таблице 7.4 представлены данные о распределении по полу работников двух предприятий в составе одного акционерного общества. Сравним вариацию работников по полу на этих предприятиях.
Таблица 7.4
| № п/п | Число занятых, чел. | ||
| всего | в том числе | ||
| мужчин | женщин | ||
| Итого |
Решение.
За основу расчета возьмем значение пола «мужской» и рассчитаем долю мужчин на каждом предприятии:
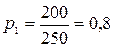 ;
;
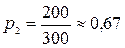 .
.
Тогда значения дисперсии доли для предприятий
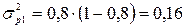 ;
;
 .
.
Согласно полученным значениям дисперсии доли вариация работников по полу на первом предприятии ниже, чем на втором.
Правило сложения дисперсий
На практике часто единицы наблюдения, являющиеся носителем исследуемого количественного признака, одновременно могут быть сгруппированы по другому признаку. Пример такой двумерной группировки представлен в таблице 7.5.
Таблица 7.5
Распределение обучающихся на курсе по возрасту и учебным группам, чел.
| № группы | Возраст, лет | Итого | |||
| Итого |
В подобных случаях при изучении вариации исследуемого признака (например, возраста) наряду с его общей дисперсией могут быть рассчитаны внутригрупповые дисперсии (внутри каждой учебной группы) и межгрупповая дисперсия.
Внутригрупповая дисперсия характеризует вариацию исследуемого признака в рамках отдельной группы. При этом учитывается влияние всех возможных факторов, в том числе и неучтенных при проведении статистического наблюдения, но исключается влияние признака, по которому выделены группы.
Внутригрупповая дисперсия определяется по формуле
 ,
,
где:
xj – варианты значения признака x в j -ой группе;
fj – соответствующие этим вариантам частоты;
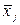 – среднее значение признака x в рамках j-ой группы, которое рассчитывается по формуле средней арифметической взвешенной
– среднее значение признака x в рамках j-ой группы, которое рассчитывается по формуле средней арифметической взвешенной
 .
.
Межгрупповая дисперсия оценивает вариацию внутригрупповых средних значений исследуемого признака относительно общего среднего значения. По сути, она характеризует вариацию этого признака только под влиянием значений группировочного признака.
Межгрупповая дисперсия рассчитывается по формуле
 ,
,
где:
nj – число единиц в j -ой группе;
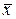 – общее среднее значение исследуемого признака, которое может быть рассчитано путем осреднения внутригрупповых средних значений по формуле
– общее среднее значение исследуемого признака, которое может быть рассчитано путем осреднения внутригрупповых средних значений по формуле
 .
.
Общая дисперсия учитывает влияние на вариацию признака всех существующих факторов и может быть рассчитана по правилу сложения дисперсий:
 ,
,
где:
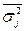 – среднее значение внутригрупповых дисперсий;
– среднее значение внутригрупповых дисперсий;
 .
.
Пример 7.3. Рассчитаем общую дисперсию возраста обучающихся (таблица 7.5), используя правило сложения дисперсий.
Итерационную часть расчета отразим в таблицах 7.6, 7.7, 7.8, 7.9, а полученные в них итоговые значения подставим в используемые при расчете формулы.
На основе итоговых значений из таблиц 7.6, 7.7 рассчитаем внутригрупповые значения среднего возраста и дисперсии.
Таблица 7.6
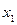
| 
|  
| 
|  
|
| Итого | – |
Таблица 7.7
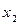
| 
|  
| 
|  
|
| Итого | – |
Средней возраст обучающихся в каждой учебной группе:
 лет;
лет;
 лет.
лет.
Внутригрупповые дисперсии возраста:
 ;
;
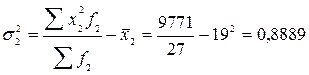 .
.
На основе данных таблицы 7.8 рассчитаем среднее значение внутригрупповых дисперсий и общий средний возраст обучающихся.
Таблица 7.8

| 
|  
| 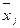
| 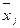 
| 
|  
|
| 1,0400 | 26,0000 | |||||
| 0,8889 | 24,0003 | |||||
| Итого | 50,0003 | – | – |
Среднее значение внутригрупповых дисперсий
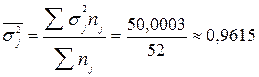 .
.
Общий средний возраст обучающихся на курсе
 лет.
лет.
Таблица 7.9
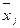
| 
| 
| 
| 
|
| -0,52 | 0,2704 | 6,7600 | ||
| 0,48 | 0,2304 | 6,2208 | ||
| Итого | – | – | 12,9808 |
На основе данных таблицы 7.9 рассчитаем межгрупповую дисперсию доли
 .
.
Тогда общая дисперсия возраста составляет
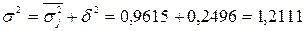 .
.
Согласно полученным значениям дисперсий, можно сделать вывод, что вариация возраста обучающихся слабо зависит от того, в какой учебной группе они учатся. Об этом говорит низкое значение межгрупповой дисперсии (низкое – относительно среднего уровня внутригрупповых дисперсий). Таким образом, вариация возраста в основном зависит от прочих факторов, оставшихся за границами исходных данных задачи.
Необходимо отметить, что аналогичное правило сложения дисперсий существует для вариации значений альтернативного атрибутивного признака. В этом случае дисперсии доли рассчитывают по следующим формулам:
· внутригрупповая дисперсия доли
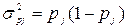 ,
,
где 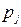 – значение доли одного из значений признака в j -ой группе;
– значение доли одного из значений признака в j -ой группе;
· межгрупповая дисперсия доли
 ,
,
где:
 – значение доли одного из значений признака во всей статистической совокупности;
– значение доли одного из значений признака во всей статистической совокупности;
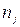 – число единиц в j -ой группе;
– число единиц в j -ой группе;
· общая дисперсия доли
 ,
,
где:
 – среднее значение внутригрупповых дисперсий доли;
– среднее значение внутригрупповых дисперсий доли;
 .
.
Пример 7.4. В таблице 7.10 представлено распределение работников учебного управления вуза по структурным подразделениям и по полу.
Таблица 7.10
| Структурное подразделение | Число сотрудников, чел. | ||
| всего | в том числе | ||
| мужчины | женщины | ||
| Отдел планирования учебного процесса | |||
| Отдел контроля и анализа учебного процесса | |||
| Итого |
Рассчитаем общую (для всего управления) и внутригрупповые (в рамках отдельного подразделения) дисперсии доли сотрудников-мужчин, а затем, используя правило сложения дисперсий, определим величину межгрупповой дисперсии доли и сделаем вывод о степени влияния места работы в рамках управления на вариацию сотрудников по полу.
Решение.
Общая доля мужчин
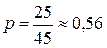 .
.
Общая дисперсия доли мужчин
 .
.
Внутригрупповые доли мужчин:
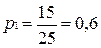 ;
;
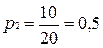 .
.
Внутригрупповые дисперсии доли мужчин:
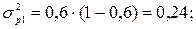
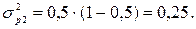
Среднее значение внутригрупповых дисперсий доли:
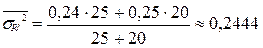 .
.
Межгрупповая дисперсия доли мужчин:
 .
.
Таким образом, вариация сотрудников по полу в рамках учебного управления практически не зависит от того, в каком именно структурном подразделении управления они работают, и целиком определяется другими факторами.
Относительные показатели вариации
Для сравнения вариации разных количественных признаков или одного и того же признака, но в разных статистических совокупностях недостаточно знать значения абсолютных показателей вариации. Чтобы сравнение было объективным, любой абсолютный показатель вариации надо соотносить с общим уровнем варируемого признака, который, в свою очередь, оценивается его средним значением.
Учитывая данный подход, при проведении статистического сравнительного анализа вариации принято рассчитывать следующие относительные показатели:
· коэффициент осцилляции
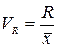 ,
,
где:
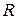 – размах вариации количественного признака х.
– размах вариации количественного признака х.
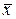 – среднее значение этого признака;
– среднее значение этого признака;
· линейный коэффициент вариации
 ,
,
где 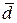 – среднее линейное отклонение значений признака х относительно его среднего значения;
– среднее линейное отклонение значений признака х относительно его среднего значения;
· коэффициент вариации
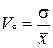 ,
,
где 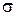 – среднеквадратичное отклонение признака х.
– среднеквадратичное отклонение признака х.
Очевидно, что чем выше значение относительного показателя вариации, тем сильнее вариация значений признака.
Пример 7.5. В таблице 7.11 представлены статистические данные распределения промышленных предприятий города (ед.) по форме собственности и числу занятых. Сравним вариацию числа занятых в рамках отдельных групп предприятий, образованных по форме собственности, рассчитав все варианты относительных показателей вариации.
Таблица 7.11
| Форма собственности | Число занятых, чел. | Итого | ||||
| До 100 | 101-200 | 201-300 | 301-400 | 401-500 | ||
| Хозяйственные товарищества и общества | ||||||
| Производственные кооперативы | - | |||||
| Государственные (муниципальные) унитарные предприятия | - | |||||
| Итого |
Решение.
Итерационную часть расчета представим в таблицах 7.12, 7.13, 7.14.
Таблица 7.12
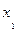
| 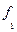
| 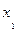 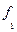
| 
|  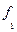
| 
|  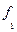
|
| Итого | - | - |
Согласно итогам, представленным в таблице 7.12, рассчитаем показатели, характеризующие средний уровень и вариацию числа занятых на предприятиях – хозяйственных товариществах:
· среднее число занятых
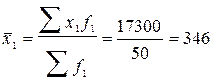 чел.;
чел.;
· размах числа занятых
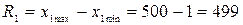 чел.;
чел.;
· коэффициент осцилляции
 ;
;
· среднее линейное отклонение числа занятых
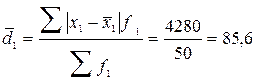 чел.;
чел.;
· коэффициент линейной вариации
 ;
;
· среднеквадратичное отклонение числа занятых
 чел.;
чел.;
· коэффициент вариации
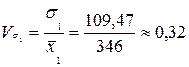 .
.
Аналогичные показатели рассчитаем для производственных кооперативов и государственных (муниципальных) унитарных предприятий, используя данные таблиц 7.13 и 7.14 соответственно.
Таблица 7.13
| 
| 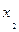 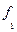
| 
|  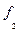
| 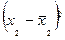
| 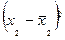 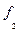
|
| 73,33 | 1099,95 | 5377,2889 | 80659,3335 | |||
| 26,67 | 266,70 | 711,2889 | 7112,8890 | |||
| 126,67 | 380,01 | 16045,2889 | 48135,8667 | |||
| 226,67 | 453,34 | 51379,2889 | 102758,5778 | |||
| Итого | - | 2200,00 | - | 238666,6670 |
Таблица 7.14
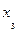
| 
| 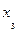 
| 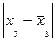
| 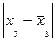 
| 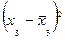
| 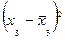 
|
| Итого | - | - |
 чел.
чел.
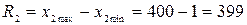 чел.
чел.
 ;
;
 чел.
чел.
 .
.
 чел.
чел.
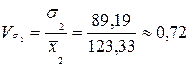 .
.
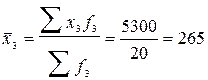 чел.
чел.
 чел.
чел.
 .
.
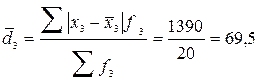 чел.
чел.
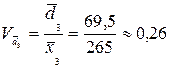 .
.
 чел.
чел.
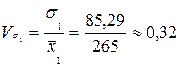 .
.
Для наглядности представим результаты расчета относительных показателей вариации в таблице 7.15.
Таблица 715
| Форма собственности | Относительные показатели вариации числа занятых | ||
| Коэффициент осцилляции | Коэффициент линейной вариации | Коэффициент вариации | |
| Хозяйственные товарищества и общества | 1,44 | 0,27 | 0,32 |
| Производственные кооперативы | 3,24 | 0,59 | 0,72 |
| Государственные (муниципальные) унитарные предприятия | 1,51 | 0,26 | 0,32 |
Данные таблицы 7.15 позволяют сделать следующие выводы:
· наиболее сильная вариация числа занятых наблюдается на предприятиях – производственных кооперативах, причем ее уровень более чем в два раза превышает уровень вариации числа занятых на предприятиях с другой формой собственности;
· уровни вариации числа занятых на предприятиях – хозяйственных товариществах и государственных (муниципальных) унитарных предприятиях практически одинаковы.
Необходимо отметить, что коэффициент осцилляции дает более грубую оценку вариации по сравнению с другими коэффициентам. Причина этого в том, что используемый при его расчете показатель размаха вариации учитывает только минимальное и максимальное значения признака и не зависит от остальных его значений.
При расчете коэффициента линейной вариации и коэффициента вариации используются показатели среднего линейного отклонения и среднеквадратичного отклонения, которые учитывают все значения признака. Это делает оценку вариации на основе этих коэффициентов более точной.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2155; Нарушение авторских прав?; Мы поможем в написании вашей работы!