Тыс. руб./чел

.

Предельная ошибка среднего диаметра

.

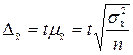При доверительной вероятности P = 0,683 табличное значение коэффициента доверия t = 1.

Выборочная дисперсия диаметра деревьев

.

Итерационную часть расчетов представим в таблице 8.3.

Таблица 8.3

Итого			–

Согласно данным итоговой строке таблицы 8.3:

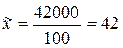см;

;

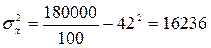≈ 12,7 см;

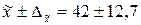= 29,3; 54,7 см.

Таким образом, с вероятностью 0,683 можно утверждать, что средний диаметр деревьев в лесу находится в пределах от 29,3 до 54,7 см.

При большом объёме выборочной совокупности механическое наблюдение близко к бесповторному собственно-случайному отбору. Действительно, если, например, совокупность людей большого объема предварительно упорядочить по их фамилиям в алфавитном порядке и отобрать каждого k -го человека, то нельзя заранее узнать, кто из первоначальной неупорядоченной совокупности попадет в выборку, а кто – нет. Следовательно, по своей сути такой отбор будет носить случайный характер, но с той лишь разницей, что он всегда будет бесповторным. Поэтому для механической выборки могут быть применены формулы расчёта средней ошибки бесповторной собственно-случайной выборки.

Пример 8.2. Статистическим управлением города для изучения общественного мнения о работе городской администрации в порядке механического отбора было опрошено 6400 чел., что составило 2 % населения города. Из числа опрошенных 3840 чел. положительно оценили работу администрации. Определим с вероятностью 0,954 пределы, в которых находится доля городского населения, положительно оценивающего работу администрации.

Решение.

Границы доли населения, положительно оценивающего работу администрации

.

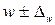Выборочная доля населения

.

Предельная ошибка доли населения

.

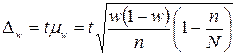При доверительной вероятности Р = 0,954 табличное значение коэффициента доверия t = 2.

Поскольку доля опрошенных людей от всего населения города составила 2 %, то

.

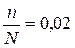Тогда

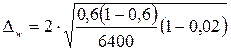≈ 0,012;

0,588; 0,612.

Таким образом, с вероятностью 0,954 можно утверждать, что от 58,8 до 61,2 % населения города положительно оценивают работу городской администрации.

При типическом наблюдении средняя ошибка выборки определяется по следующим формулам:

· при повторном отборе

;

;

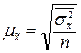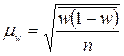· при бесповторном отборе

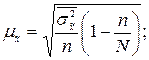
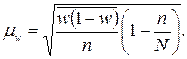
где:

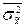– среднее значение внутригрупповых выборочных дисперсий;

– среднее значение внутригрупповых выборочных дисперсий доли.

Условием применения этих формул является пропорциональный отбор единиц в типические группы, основанный на выполнении условия

,

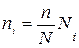где:

n_i, N_i – число единиц в i -ой выборочной и i -ой генеральной типических группах.

Пример 8.3. С целью выявления удельного веса простоев из-за несвоевременного поступления на предприятие комплектующих изделий было проведено одномоментное выборочное наблюдение рабочих трёх цехов на основе 20%-го случайного бесповторного отбора. Результаты наблюдения представлены в таблице 8.4.

Таблица 8.4

№ цеха	Объём выборки, чел.	Удельный вес простоев
		0,15
		0,10
		0,08
Итого		–

Определим с вероятностью 0,997 пределы, в которых находится удельный вес простоев рабочих из-за несвоевременного поступления комплектующих на предприятие в целом.

Решение.

Имеет место типический бесповторный отбор рабочих (номер цеха – это типологический признак рабочего).

Пределы удельного веса простоев

.

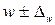Общий удельный вес простоев

.

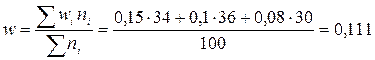Предельная ошибка удельного веса простоев

.

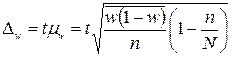Среднее значение внутригрупповых дисперсий удельного веса простоев

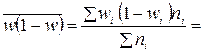
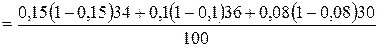≈ 0,098.

При доверительной вероятности Р = 0,997 табличное значение коэффициента доверия t = 3.

Доля опрошенных рабочих в каждом цехе и, следовательно, на всем предприятии составила 20%, поэтому

.

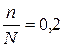Тогда

;

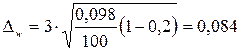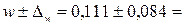0,027; 0,185.

Таким образом, с вероятностью 0,997 можно утверждать, что удельный вес простоев рабочих из-за несвоевременного поступления комплектующих на предприятие в целом находится в пределах от 0,027 до 0,185.

Пример 8.4. В таблице 8.5 представлены результаты выборочного 10%-го механического наблюдения предприятий отрасли, сгруппированных по форме собственности и величине фондовооруженности. Определим с вероятностью 0,954 пределы, в которых находится среднее значение фондовооруженности предприятий отрасли.

Таблица 8.5

Форма собственности предприятия	Фондовооруженность, тыс. руб./чел.	Итого
500 – 1000	1000 – 1500	1500 – 2000
Хозяйственные товарищества
Производственные кооперативы
Государственные (муниципальные) унитарные предприятия
Итого

Решение.

Имеет место типический механический отбор (отбираемые предприятия предварительно сгруппированы в типические группы по форме собственности).

Пределы средней фондовооруженности

.

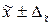Выборочная средняя фондовооруженность

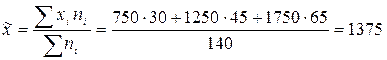тыс. руб./чел.

Предельная ошибка средней фондовооруженности

.

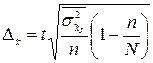Среднее значение внутригрупповых дисперсий фондовооруженности

,

где 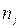, 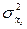– число предприятий и дисперсия их фондовооруженности в рамках j -ой группы.

Внутригрупповые дисперсии фондовооруженности

.

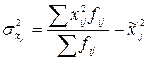Внутригрупповые средние значения фондовооружённости:

;

тыс. руб./чел.;

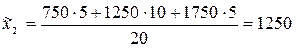тыс. руб./чел.;

≈ 1393 тыс. руб./чел.

Тогда:

;

;

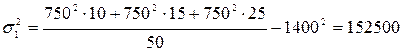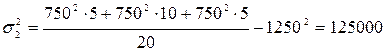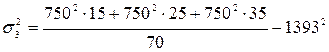≈ 157765;

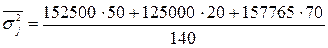≈ 151204.

При доверительной вероятности P = 0,954 табличное значение коэффициента доверия: t = 2.

Доля предприятий отрасли, попавших в выборку, составляет 10%, поэтому

.

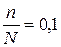Тогда:

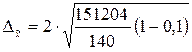≈ 62 тыс. руб./чел.;

Таким образом, с вероятностью 0,954 можно утверждать, что среднее значение фондовооруженности предприятий отрасли находится в пределах от 1313 до 1437 тыс. руб./чел.

При серийном наблюдении для расчета средней ошибки выборки используют следующие формулы:

· при повторном отборе

;

;

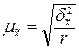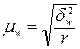· при бесповторном отборе

;

,

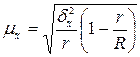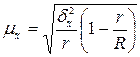где:

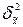– межсерийная выборочная дисперсия;

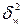– межсерийная выборочная дисперсия доли;

r – число отобранных серий;

R – число серий в генеральной совокупности.

Пример 8.5. С целью проверки качества радиоэлектронной продукции из двадцати равновеликих партий микросхем случайным бесповторным образом отобрали пять партий. В каждой из них подвергли проверке все микросхемы. В результате проверки доля бракованных микросхем в отдельных партиях составила 5; 6; 4; 2 и 3 % соответственно. Определим с вероятностью 0,997, в каких пределах находится доля бракованных микросхем во всех двадцати партиях.

Решение.

Имеет место серийный бесповторный отбор.

Границы генеральной доли бракованных микросхем

.

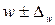Общая выборочная доля бракованных микросхем

.

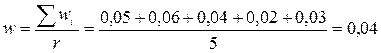Предельная ошибка выборочной доли бракованных микросхем

.

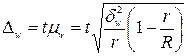Поскольку доверительная вероятность P = 0,997, то t = 3.

Межсерийная дисперсия доли бракованных микросхем

.

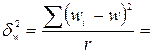
Тогда

;

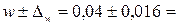0,024; 0,056.

Таким образом, с вероятностью 0,997 можно утверждать, что доля бракованных микросхем в целом во всех партиях находится в пределах от 2,4 до 5,6 %.

Пример 8.6. Для оценки качества работы конвейерной машины по расфасовке сахарного песка подвергли сплошному наблюдению упаковки сахарного песка в трёх контейнерах одинакового объёма. Эти контейнеры были отобраны механическим образом из девяти имеющихся в наличии. В результате наблюдения была определена средняя масса одной упаковки сахарного песка в каждом контейнере. Её величина составила соответственно 995; 1050, 1010 грамм. Определим с вероятностью 0,954 пределы, в которых находится средняя масса упаковки сахарного песка во всех девяти контейнерах.

Решение.

Границы средней массы одной упаковки

.

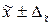Общая выборочная средняя масса одной упаковки

г.

Предельная ошибка средней массы одной упаковки

.

При доверительной вероятности P = 0,954 коэффициент доверия t = 2.

Межсерийная дисперсия средней массы одной упаковки

.

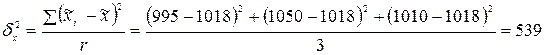Тогда:

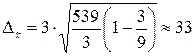г;

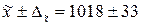= 985; 1051 г.

Таким образом, с вероятностью 0,954 можно утверждать, что средняя масса одной упаковки сахарного песка во всех имеющихся в наличии контейнерах находится в пределах от 985 до 1051 г.

Определение необходимого объёма выборки

Перед проведением выборочного наблюдения необходимо определить объём будущей выборочной совокупности. Выбор объёма осуществляют, задаваясь точностью результатов наблюдения (предельной ошибкой выборки) и их достоверностью (доверительной вероятностью или коэффициентом доверия).

В таблице 8.6 представлены формулы расчёта необходимого объёма выборки при различных способах наблюдения. Применение этих формул требует знания выборочных дисперсий – общей, внутригрупповых или межсерийной. Их значения можно взять из результатов аналогичного наблюдения, проведённого ранее. Если такой возможности нет, то необходимо провести предварительное выборочное наблюдение небольшого объёма и по его результатам рассчитать выборочные дисперсии.

Пример 8.7. Планируется проведение собственно-случайного повторного наблюдения проб угля месторождения с целью определения его средней зольности (в %). При наблюдении аналогичного месторождения среднеквадратичное отклонение зольности угля составило 3%. Определим необходимое число проб угля для определения средней зольности всего месторождения наблюдения с точностью ±0,5% и доверительной вероятностью 0,954.

Таблица 8.6

Способ наблюдения	Исследуемый показатель	Метод наблюдения
повторный	бесповторный
Собственно-случайный	Среднее значение
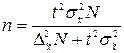
Доля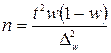
Механический	Среднее значение	–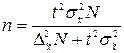
Доля	–
Типический	Среднее значение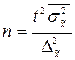
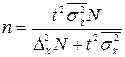
Доля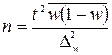
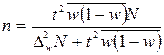
Серийный	Среднее значение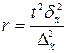
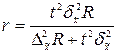
Доля

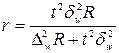
Решение.

Необходимый объем выборки

.

При доверительной вероятности P = 0,954 коэффициент доверия t = 2.

Тогда

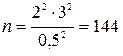пробы.

Таким образом, чтобы определить среднюю зольность угля всего месторождения с точностью ± 3% и гарантировать этот результат с вероятностью 0,954, необходимо подвергнуть собственно-случайному повторному наблюдению 144 пробы угля.

Пример 8.8. Необходимо провести серийное бесповторное наблюдение партии говяжьей тушёнки с целью определения средней массы одной банки. Партия состоит из 100 упаковок. При проверке предыдущей аналогичной партии было обследовано пять упаковок тушенки. При этом в каждой упаковке средняя масса банки составила соответственно 320; 323; 327 и 330 г. Определим, сколько упаковок надо обследовать в текущей партии, чтобы получить результат с точностью ± 3 г и доверительной вероятностью 0,683.

Решение.

Необходимый объём выборки

.

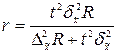При доверительной вероятности P = 0,683 коэффициент доверия t = 1.

Межсерийная дисперсия средней массы банки тушенки по данным предыдущего наблюдения

.

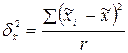Общая средняя масса банки тушенки по данным предыдущего наблюдения

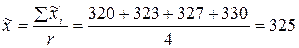г.

Тогда:

.

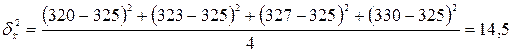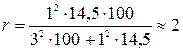упаковки.

Таким образом, чтобы определить среднюю массу банки говяжьей тушёнки во всей партии с точностью ± 3 г и гарантировать этот результат с вероятностью 0,683, необходимо подвергнуть сплошному наблюдению банки из двух упаковок, отобрав эти упаковки механически или случайно-бесповторно.

Пример 8.9. В отчетном году планируется провести выборочное повторное наблюдение сотрудников государственной противопожарной службы рядового и младшего начальствующего состава, проходящих службу на территории Санкт-Петербурга и Ленинградской области, с целью определения доли сотрудников, удовлетворённых условиями своей службы. По результатам аналогичного опроса в предшествующем году были получены следующие значения доли сотрудников, удовлетворённых условиями своей службы: рядовой состав – 45%; младший начальствующий состав – 55%. При этом число опрошенных каждой категории сотрудников было одинаковым. Определим, сколько требуется опросить сотрудников, чтобы точность результатов наблюдения составила ± 5 % с доверительной вероятностью 0,954.

Решение.

Имеет место типическое повторное наблюдение.

Необходимый объём наблюдения

.

При доверительной вероятности P = 0,954 коэффициент доверия t = 2.

Среднее значение внутригрупповой дисперсии доли по данным прошлого наблюдения

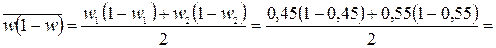
= 0,2475.

Тогда

чел.

Таким образом, опросив 396 человек из числа сотрудников государственной противопожарной службы (198 человек рядового состава и 198 человек младшего начальствующего состава) и рассчитав на основе результатов опроса общую долю сотрудников, удовлетворённых условиями своей службы, можно гарантировать точность значения этого показателя на уровне ± 5 % с доверительной вероятностью 0,954.

Лекция 6 КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ

Дата добавления: 2014-01-07