Непараметрический корреляционный анализ

Методы изучения парной и множественной корреляции количественных признаков, рассмотренные в параграфе 9.3, называют параметрическими, так как они предполагают вычисление таких параметров вариации, как среднее значение признака и его дисперсия. В ряде случаев, когда речь идет о взаимосвязи атрибутивных признаков или подлежащих ранжированию количественных признаках, вместо указанных методов можно использовать более простые непараметрические методы корреляционного анализа.

Рассмотрим самый простой вариант, когда надо оценить связь между двумя атрибутивными альтернативными признаками:

;

.

В этом случае результаты наблюдения заносят в специальную таблицу (таблица 9.11).

Таблица 9.11

Варианты признаков	А 1	А 2	Итого
В 1	a	b	a+b
В 2	c	d	c+d
Итого	a+c	b+d	n

В представленной таблице а, b, с, d – это число наблюдений, при которых сочетаются определенные значения признаков А и B, а n – общее число наблюдений.

Затем рассчитывают на выбор один из двух показателей:

· коэффициент ассоциации

;

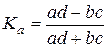· коэффициент контингенции

.

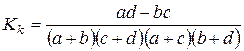Значение этих коэффициентов находятся в пределах от –1 до 1. Их знак указывает на направление связи между признаками: положительный – прямая связь, отрицательный – обратная. Чем ближе абсолютное значение коэффициентов к 1, тем сильнее связь. Связь считается подтвержденной, если:

;

.

В общем случае при неизменных результатах наблюдения всегда выполняется условие

.

Пример 9.7. В таблице 9.12 представлены данные о распределении респондентов (тыс.чел.) по признакам потребления наркотиков и семейного положения.

Таблица 9.12

Группы респондентов по отношению к потреблению наркотиков	Семейное положение	Всего
замужем (женат)	не замужем (не женат)
Потреблял наркотики	10,1	14,4	24,5
Не потреблял	2,4	4,6	7,0
Всего	12,5	19,0	31,5

Оценим зависимость потребления наркотиков от семейного положения, рассчитав коэффициенты ассоциации и контингенции.

Решение.

.

.

, .

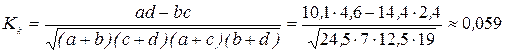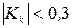Таким образом, оба коэффициента указывают на отсутствие существенной связи между потреблением наркотиков респондентом и его семейным положением.

Пример 9.8. В таблице 9.13 представлены данные опроса работников предприятия (чел.). Оценим зависимость удовлетворенности своей работой от уровня образования работника, рассчитав коэффициенты ассоциации и контингенции.

Таблица 9.12

Группы работников по уровню образования	Удовлетворенность своей работой	Итого
удовлетворены	не удовлетворены
Высшее
Средние
Итого

Решение.

.

.

, .

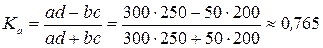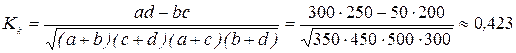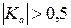Таким образом, оба коэффициента показывают, что между уровнем образования работника и удовлетворенностью своей работой имеется существенная связь, причем, чем выше уровень образования, тем сильнее удовлетворенность своей работой.

Если анализируемые атрибутивные признаки имеют произвольное число значений:

;

,

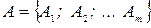то для оценки связи между ними рассчитывают коэффициенты взаимной сопряженности Пирсона и Чупрова.

Вначале по результатам наблюдения заполняют специальную таблицу (таблица 9.13), в которой:

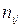– число единиц наблюдения, у которых сочетаются значения признаков 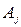и ;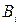

n – общее число единиц наблюдения.

Таблица 9.13

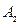
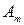
Варианты признаков			…		Итого
			…
			…
…	…	…	…	…	…
			…
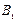
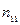
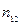
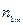
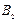
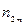
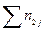
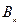
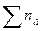
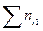
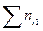
Итого			…		n

Затем рассчитывают показатель взаимной сопряженности

.

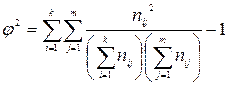Полученное значение 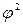используют для расчета одного из коэффициентов сопряженности:

коэффициент Пирсона

;

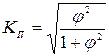коэффициент Чупрова

.

Значения обоих коэффициентов находятся в пределах от 0 до 1. Чем ближе эти значения к 1, тем сильнее связь между признаками.

Пример 9.9. В таблице 9.14 представлены данные опроса граждан государств с различным типом государственного управления (тыс. чел., цифры условные). Рассчитаем коэффициенты Пирсона и Чупрова и сделаем вывод о зависимости жизненного уровня граждан страны от типа государственного управления.

Таблица 9.14

Тип государственного управления	Жизненный уровень респондента	Итого
высокий	средний	низкий	за чертой бедности
Президентская республика	1,3	41,0	50,0	6,0	98,3
Парламентская республика	0,4	25,0	57,0	14,0	96,4
Парламентская республика с президентом	1,5	26,0	58,0	14,0	99,5
Конституционная монархия	0,2	25,0	60,0	15,0	100,2
Советская социалистическая республика	0,2	19,0	63,0	18,0	100,2
Итого	3,6	136,0	288,0	67,0	494,6

Решение.

Вначале рассчитаем показатель взаимной сопряженности:

.

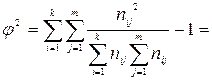
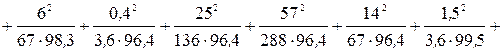
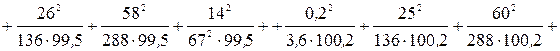
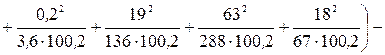
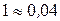На основе показателя взаимной сопряженности рассчитаем значения коэффициентов Пирсона и Чупрова:

;

.

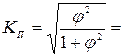
Относительная близость значений обоих коэффициентов к нулю свидетельствует об отсутствии существенной связи между уровнем жизни населения страны и типом ее государственного управления.

Оценку корреляции количественных признаков, значения которых подлежат ранжированию, можно существенно упростить, используя для этого методы ранговой корреляции.

Ранжирование значений признаков проводят единообразно – по возрастанию значений или убыванию. Пример такого ранжирования представлен в таблице 9.15.

Таблица 9.15

Ранжирование предприятий по числу занятых

Число занятых, чел. (х)						Итого
Ранг предприятия (Rх)

Если наблюдаются одинаковые значения признака, то им присваивают одинаковые ранги так, чтобы сумма всех рангов оставалась неизменной (таблица 9.16).

Таблица 9.15

Ранжирование предприятий по числу занятых

Число занятых, чел. (х)						Итого
Ранг предприятия (Rх)	1,5	1,5	4,5		4,5

Для оценки корреляции двух ранжированных признаков рассчитывают коэффициент Спирмена, используя одну из формул:

· при отсутствии одинаковых рангов

;

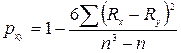· при наличии одинаковых рангов

,

где:

, значения рангов признака 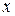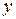и соответственно;

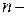число наблюдений.

Параметры 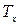и определяют по формуле:

,

где:

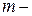число групп одинаковых рангов;

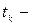число рангов в 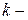ой группе.

Коэффициент Спирмена принимает значения от –1 до 1. При прямой связи он положителен, при обратной – отрицателен. Чем ближе абсолютное значение коэффициента к 1, тем связь сильнее. Связь признается существенной, если .

При ограниченном числе наблюдений проверяют достоверность вывода о существенной связи, используя критерий Стьюдента. Проверку осуществляют так же, как и при оценке парной корреляции не ранжированных значений признаков, используя аналогичное условие

.

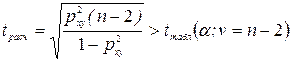Если условие выполняется, то полученное высокое значение коэффициента Спирмена признается значимым с вероятностью .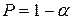

Пример 9.10. На основе исходных данных примера 9.1 присвоим предприятиям ранги, исходя из стоимости реализованной ими продукции и величины балансовой прибыли. Оценим направление и тесноту связи между этими признаками, используя коэффициент ранговой корреляции Спирмена.

Решение.

Итерационную часть решения задачи раскроем в таблице 9.16.

Таблица 9.16.

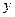
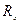
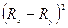
49,1	13,2
53,2	15,7			-1
54,8	15,3
60,3	19,0
65,4	19,5
66,0	21,0
69,7	21,4
72,4	23,7			-1
73,0	23,0
75,0	25,1
Итого			-

Учитывая отсутствие одинаковых рангов, величина коэффициента

.

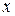Поскольку , то между признаками и 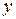существует прямая существенная корреляционная зависимость.

Оценим достоверность этого утверждения, используя критерий Стьюдента:

;

.

Поскольку 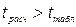, то утверждение о наличие существенной связи между признаками гарантируется с вероятностью .

При изучении корреляции трех и более ранжированных количественных признаков рассчитывают коэффициент конкордации, используя одну из формул:

· при отсутствии одинаковых рангов

;

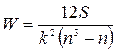· при наличии одинаковых рангов

,

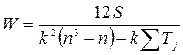где:

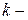число признаков, имеющих одинаковые значения и, соответственно, одинаковые ранги;

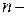число наблюдений.

Параметр 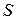определяют по формуле

,

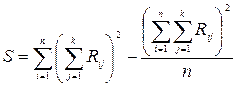где 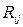– ранг 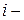го значения 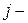го признака.

Параметр 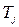определяют для каждого 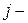го признака, имеющего одинаковые ранги, по формуле

,

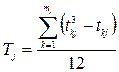где:

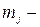число групп одинаковых рангов значений 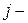го признака;

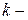число рангов в ой группе для 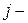го признака.

Коэффициент конкордации принимает значение от 0 до 1. Чем ближе его величина к 1, тем связь между признаками сильнее. Связь признается существенной, если .

Достоверность вывода о существенной связи между ранжированными значениями количественных признаков проверяют по критерию Пирсона, используя значения 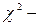распределения и условие

.

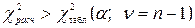Расчетное значение критерия вычисляют по одной из формул:

· при отсутствии одинаковых рангов

;

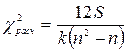· при наличии одинаковых рангов

.

Интерпретация критерия Пирсона аналогична интерпретации критерия Стьюдента, применяемого при оценке парной ранговой корреляции.

Пример 9.11. В таблице 9.17 представлены результаты ранговой экспертной оценки степени зависимости устойчивости организации к изменениям экономической конъюнктуры от следующих финансовых показателей:

· коэффициента общей финансовой независимости организации ();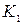

· коэффициента финансовой независимости при формировании оборотных средств ();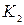

· коэффициента финансовой независимости при формировании запасов и затрат ();

· коэффициента абсолютной ликвидности имущества ();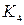

· коэффициента средней ликвидности ();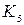

· коэффициента текущей ликвидности ().

Таблица 9.17

Показатель	Номер эксперта
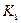
						1,5
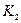
		2,5				1,5
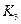
		2,5
				5,5
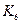
				5,5

Оценим степень согласованности мнений экспертов, рассчитав на основе представленных данных коэффициент конкордации.

Решение.

Учитывая наличие одинаковых рангов, для расчета коэффициента конкордации используем следующие формулы:

;

;

.

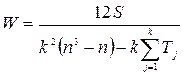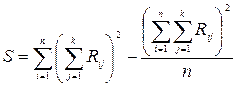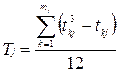Итерационную часть расчета представим в таблице 9.18.

Таблица 9.18

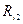
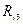
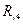
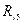
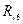
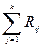
					1,5	6,5	42,25
	2,5				1,5	12,0	144,00
	2,5					18,5	342,25
						24,0	576,00
			5,5			29,5	870,25
			5,5			35,5	1260,25
						126,0	3235,00

Тогда:

;

;

;

;

;

.

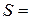
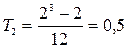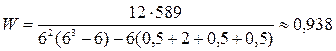Поскольку , то мнения экспертов обладают высокой степенью согласованности. Оценим достоверность этого вывода по критерию Пирсона.

Учитывая наличие одинаковых рангов, расчетное значение критерия Пирсона составляет

.

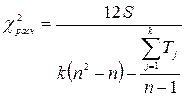
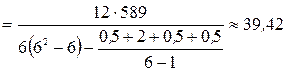Табличное значение критерия

.

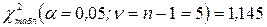Условие 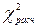> выполняется. Следовательно, вывод о высокой степени согласованности мнений экспертов гарантируется с вероятностью .

Дата добавления: 2014-01-07