Функции. Вычеты. Нули аналитической функции

Нули аналитической функции.
Определение. Точка а называется нулём порядка k аналитической функции f (z), если f (a) = f ′(a) = f ″(a) =... = f ^{( k −1)}(a) = 0, но f ^{( k )}(a) ≠ 0.
Пример. Пусть . Точка a = 0 - нуль этой функции, так как f (0) = 0. Найдём порядок нуля: f ″(z) = − sin z + z, f ″(0)= 0, f ⁽³⁾(z) = − cos z + 1, f ⁽³⁾(0) = 0, f ⁽⁴⁾(z) = sin z, f ⁽⁴⁾(0) = 0, f ⁽⁵⁾(z) = cos z, f ⁽⁵⁾(0) = 1 ≠ 0,. Первая отличная от нуля производная функции в точке a = 0 - пятая, поэтому эта точка - нуль пятого порядка функции .
Теорема. Для того, чтобы аналитическая в точке а функция f (z) имела в этой точке нуль k -го порядка, необходимо и достаточно, чтобы в окрестности этой точки функция f (z) представлялась в виде f (z) = (z − a) ^k · φ (z), где φ (z) - аналитическая в точке а функция, и φ (a) ≠ 0.
Доказательство. Необходимость. Пусть точка а - нуль k -го порядка функции f (z), т.е. f (a) = f ′(a) = f ″(a) =... = f ^{( k −1)}(a) = 0, и f ^{( k )}(a) ≠ 0. Тогда её разложение в ряд Тейлора имеет вид 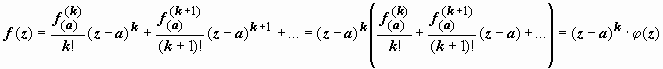, где - аналитическая (как сумма степенного ряда с тем же кругом сходимости, что и у ряда для f (z)) функция, .
Достаточность. Пусть f (z) = (z − a) ^k · φ (z), где φ (z) - аналитическая в точке а функция, и φ (a) ≠ 0. Находим производные этой функции по формуле Лейбница (uv) ^{( n )} = u ^{( n )} v + nu ^{( n - 1)} v ′ + C_n ² u ^{( n - 2)} v ″ + C_n ³ u ^{( n - 3)} v ⁽³⁾ + … + C_n ² u ″ v ^{( n - 2)} + n u ′ v ^{( n - 1)} + uv ^{( n )}: f ′(z) = k (z − a) ^{k - 1} φ (z) + (z − a) ^k φ ′(z), f ′(a) = 0; f ″(z) = k (k − 1)(z − a)^{( k - 2)} φ (z) + 2 k (z − a)^{( k - 1)} φ ′(z) + (z − a)^{( k )} φ ″(z), f ″(a) = 0;
…………… ………………………….;
f ^{( k -1)}(z) = k ·(k -1)·…2·(z − a) φ (z) + C ¹ _{k -1} k ·(k -1)·…3·(z − a)² φ ′(z) + … + (z − a) ^k φ ^{(k -1)}(z), f ^{(k -1)}(a) = 0;
f ^(k)(z) = k ·(k -1)·…2·1· φ (z) + C ¹ _k k ·(k -1)·…2·(z − a) φ ′(z) + … + (z − a) ^k φ ^{( k )}(z), f ^{( k )}(a) = k!· φ (a) ≠ 0, что и требовалось доказать.
Из этой теоремы следует, что если многочлен

P _n (z) = a ₀ z ⁿ + a ₁ z ^{n - 1} + a ₂ z ^{n - 2} + … + a _{n - 1} z = 0 (1)

разложен на множители

P _n (z) = a ₀ (z − z ₁) ^k ₁ (z − z ₂) ^k ₂ … (z − z_l) ^k_l, (2)

то корни z ₁, z ₂, …, z_l являются нулями функции P _n (z) кратностей, соответственно, k ₁, k ₂, …, k_l.
Изолированные особые точки.
Определение. Точка а называется изолированной особой точкой функции f (z), если существует окрестность этой точки, в которой f (z) аналитична во всех точках, за исключением точки а.
Рассмотрим разложение функции f (z) в ряд Лорана

(3)

в окрестности изолированной особой точки а. При этом возможны следующие случаи.
1. Главная часть ряда Лорана отсутствует: 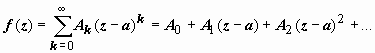. (4)
В этом случае особая точка а называется устранимой.
2. Главная часть содержит конечное число членов: 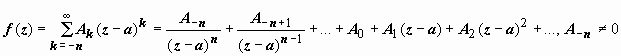. (5)
В этом случае особая точка а называется полюсом n -го порядка. Если n =1, полюс называется простым, в остальных случаях - кратным.
3. Главная часть содержит бесконечно много членов. В этом случае особая точка а называется существенно особой точкой.
Признаки особых точек по значению .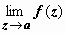
1. Для того, чтобы особая точка z = a была устранимой особой точкой функции f (z), необходимо и достаточно, чтобы существовал конечный предел 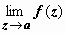= C, C ≠ ∞.
Док-во. Выпишем разложение f (z) в ряд Лорана:

.

Очевидно, что 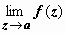может быть конечным тогда и только тогда, когда отсутствуют члены с отрицательными степенями, т.е. отсутствует главная часть, т.е. z = a – устранимая особая точка. В этом случае 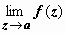= A ₀.
2. Для того, чтобы особая точка z = a была полюсом функции f (z), необходимо и достаточно, чтобы существовал бесконечный предел = ∞.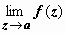
Докажем теорему, из которой следует это утверждение.
Теорема. Для того, чтобы особая точка z = a была полюсом n -го порядка функции f (z), необходимо и достаточно, чтобы в некоторой окрестности этой точки f (z) представлялась в виде 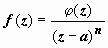, где φ (z) аналитическая в точке а функция, φ (a) ≠ 0.
Док-во. Необходимость. Пусть f (z) имеет в точке z = a была полюс n -го порядка, т.е. 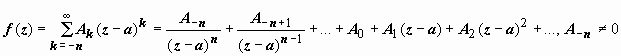. Преобразуем это выражение:

. Обозначим φ (z) сумму ряда, стоящего в скобках:

φ (z) = A _{- n} + A _{- n + 1}(z − a) + A _{- n + 2}(z − a)² + … + A ₀(z − a) ⁿ + A ₁(z − a) ^{n + 1} + A ₁(z − a) ^{n + 2} + ….
Ряд Лорана функции f (z) сходится в некотором кольце 0 < | z – a | < r. Пусть точка z ₁ принадлежит этому кольцу. Ряд для φ (z) сходится в этой точке, так как он отличается от сходящегося ряда для f (z) только постоянным множителем ; по теореме Абеля ряд для φ (z) сходится в круге | z – a | < | z ₁ – a |, и φ (z) аналитична в этом круге как сумма степенного ряда.
Достаточность. Пусть 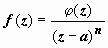, где φ (z) аналитическая в точке а функция, φ (a) ≠ 0. Разложим φ (z) в ряд Тейлора:

φ (z) = B ₀ + B ₁(z − a) + B ₂(z − a)² + … + B_k (z − a) ^k + ….

Тогда

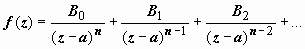, т.е. главная часть ряда Лорана функции f (z) начинается с члена 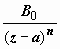, где B ₀ = φ (a) ≠ 0, т.е. точка z = a – полюс n -го порядка.
Следствие. Точка z = a – полюс n -го порядка функции f (z) тогда и только тогда, когда существует конечный

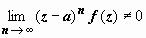. (6)
Теорема о связи нулей и полюсов. Функция f (z) имеет в точке z = a – полюс n -го порядка тогда и только тогда, когда функция 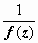имеет в этой точке нуль n -го порядка.
Это теорема непосредственно следует из доказанной теоремы и теоремы предыдущего раздела. С её помощью легко определять порядок полюса. Так, мы доказали, что функция имеет в точке 0 нуль пятого порядка. Поэтому функция имеет в этой точке полюс пятого порядка.
3. Мы доказали, что в устранимой особой точке и в полюсе существует (конечный или бесконечный) 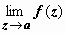. Поэтому в существенно особой точке этот предел существовать не может. Более того, верна теорема Пикара, которую мы приведём без доказательства:
В любой сколь угодно малой окрестности своей существенно особой точки функция f (z) принимает (причём бесконечно много раз) любое конечное значение (за исключением, возможно, одного).
Вычет аналитической функции в особой точке. Пусть функция f (z) аналитична в области D за исключением точки a. Разложим f (z) в окрестности этой точки в ряд Лорана: (7)
Коэффициент A _-1 называется вычетом функции f (z) в точке а и обозначается . Если γ - произвольный кусочно-гладкий замкнутый контур, расположенный в области D и содержащий внутри себя точку а, то, согласно общей формуле для коэффициентов ряда Лорана (см. 19.8.3. Ряд Лорана), получаем другое, эквивалентное, определение вычета,

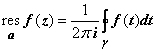= A _{- 1}. (8)
Вычет в устранимой особой точке равен нулю.
Это следует из определения устранимой особой точки: главная часть ряда Лорана отсутствует, все коэффициенты с отрицательными индексами равны нулю, A _-1 = 0.
Вычеты в полюсах.
Если а - простой полюс функции f (z), то

. (9)
Док-во. Простой полюс - полюс первого порядка, поэтому разложение в ряд Лорана начинается с минус первой степени: .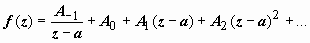

Тогда

(z − a) f (z) = A _-1 + A ₀(z − a) + A ₁(z − a) ² + A ₂(z − a) ³ + …,

.
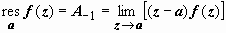Пусть , где φ (z), ψ(z) - аналитические в окрестности точки а функции. Если а - простой нуль функции ψ (z), и φ (a) ≠ 0, то

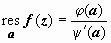. (10)
Док-во. Если а - простой нуль функции ψ (z), и φ(a) ≠ 0, то а – простой полюс функции

.

Тогда, по предыдущему утверждению, .
Если а - полюс функции f (z) n - го порядка, то . (11)
Док-во. Так как точка z = a - полюс n -го порядка функции f (z), то 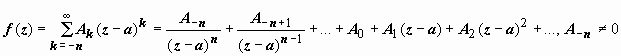. Для того, чтобы удалить особенность в точке а, умножим f (z) на (z – a) ⁿ: (z – a) ⁿf (z) = A _{- n} + A _{- n + 1}(z − a) + … + A _{- 1}(z − a) ^{n - 1} + A ₀(z − a) ⁿ + A ₁(z − a) ^{n + 1} + …. Теперь, чтобы убрать первые члены этой формулы и добраться до A _-1, дифференцируем это произведение n -1 раз: , ,
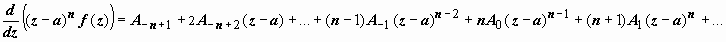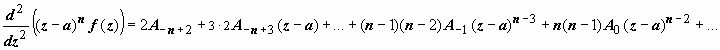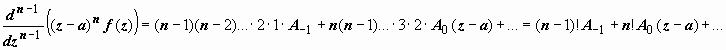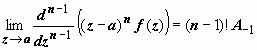, , откуда и следует доказываемая формула.
Вычет в существенно особой точке находится из разложения функции в ряд Лорана.
Примеры нахождения вычетов.
1. .
Эта функция имеет единственную особую точку - z = 0. Функция 1 – cos z при z → 0 - бесконечно малая второго порядка, (1 – cos z)² - четвертого, поэтому можно предположить, что существует конечный , т.е. z = 0 - устранимая особая точка. Доказываем строго: 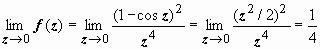z = 0 - устранимая особая точка.
Можно решить эту задачу по-другому. Так как cos z = 1 − z ² /2! + z ⁴ /4! + … + (−1) ⁿz ^{2 n} /(2 n)! + …, то (1 − cos z)² = (z ² /2! − z ⁴ /4! + … + (−1) ^{n + 1} z ^{2 n} /(2 n)! + …)² = z ⁴·(1/2! − z ² /4! + … + (−1) ^{n + 1} z ^{2 n - 2}/(2 n)! + …)², то f (z) = (1/2! − z ² /4! + … + (−1) ^{n + 1} z ^{2 n - 2}/(2 n)! + …)². Понятно, что разложение этой функции по степеням z не будет содержать членов с отрицательными степенями, т.е. z = 0 - устранимая особая точка.
2. .
Особая точка: z = 2. Разлагаем функцию в ряд по степеням z - 2:
z ² = [(z - 2) + 2] ² = (z - 2)² + 4(z - 2) + 4, , .

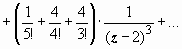Разложение содержит бесконечное количество слагаемых с отрицательными степенями z - 2, следовательно, z = 2 - существенно особая точка.

.
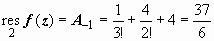3. f (z) = ctg z.
Особые точки – те, в которых sin z = 0: a_k = k π, k = 0, ±1, ±2, ±3, …. Эти точки являются простыми нулями знаменателя, так как (sin z)′| _{z = ak} = cos z | _{z = ak} = ± 1 ≠ 0. Числитель cos a_k ≠ 0, поэтому точки a_k - простые полюса. Вычеты находим по формуле

:

.
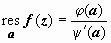4. .
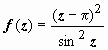Особые точки – те, в которых sin z = 0: a_k = k π. В этих точках предел знаменателя ; во всех точках a_k, за исключением a ₁ = π, числитель отличен от нуля, поэтому

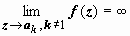, следовательно, эти точки – полюса. Для определения порядка этих полюсов найдём порядок нуля знаменателя: ψ (z) = sin ² z, ψ (a _k) = 0; ψ′ (z) = sin 2 z, ψ′ (a_k) = 0; ψ″ (z) = 2 cos 2 z, ψ′ (a_k) = 2 ≠ 0, следовательно, эти полюса имеют второй порядок (при k ≠ 1). В точке a ₁ = π функция представляет собой неопределённость 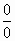, однако, если вспомнить, что sin z = sin(π − z) = − sin(z − π), эта неопределённость раскрывается просто: ,

т.е. функция имеет конечный предел, следовательно, a ₁ = π - устранимая особая точка.
Вычет в устранимой особой точке равен нулю, поэтому .

В остальных точках применяем формулу при n = 2: (меняем переменную t = z - a_k, sin z = sin(t + a_k) = sin(t + k π) = (-1) ^k sin t) =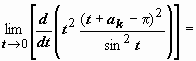

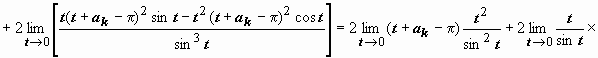
(к последнему пределу применяем правило Лопиталя) .
Основная теорема о вычетах. Пусть функция f (z) аналитична во всех точках ограниченной замкнутой области , границей которой является контур L, за исключением конечного числа особых точек z ₁, z ₂, z ₃, …, z_n, расположенных внутри L. Тогда

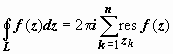. (12)
Док-во. Окружим каждую особою точку z_k, k = 1, 2, …, n контуром γ _k = { z || z − z _k | = ρ _k } таким, чтобы все контуры лежали в области D и не пересекались. В области, ограниченной контурами L, γ ₁, γ ₂, γ ₃, … γ _n, функция аналитична, поэтому по 19.5.2.2. Теореме Коши для многосвязной области 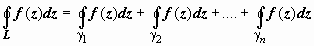. Из определения вычета следует, что 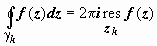, следовательно, , что и требовалось доказать.
Примеры вычисления интегралов с помощью основной теоремы о вычетах.
1. 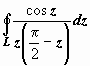, где L - квадрат | x | + | y | = 2.
Обе особые точки подынтегральной функции: z ₁= 0 и - расположены внутри контура L, поэтому .

Точка z ₁= 0 -полюс первого порядка,

.

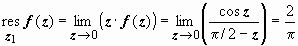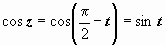Точка - нуль первого порядка и для числителя, и для знаменателя; докажем, что это - устранимая особая точка подынтегральной функции. Пусть , тогда , и

,

конечный предел существует, поэтому, действительно, это - устранимая особая точка, и 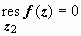. По основной теореме о вычетах .
2. 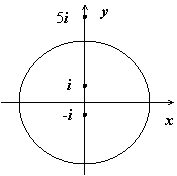. В примере 2 раздела Примеры нахождения вычетов мы доказали, что точка z = 2 - существенно особая точка подынтегральной функции, и 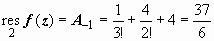, поэтому

.
3. . Здесь подынтегральная функция

имеет две особые точки, расположенные в области, находящейся внутри контура: z ₁ = i (простой полюс) и z ₂ = - i (полюс второго порядка). , ; .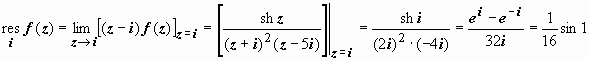
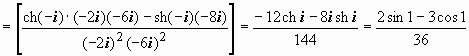4. .

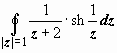Внутри контура расположена одна особая точка подынтегральной функции f (z): z = 0. Это - существенно особая точка, поэтому для нахождения вычета необходимо найти коэффициент A _-1 разложения f (z) в ряд Лорана в окрестности этой точки: ; .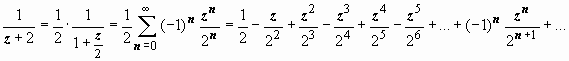
,

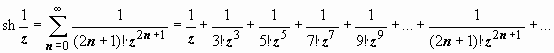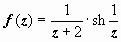однако нет необходимости выписывать произведение этих рядов, достаточно только собрать те попарные произведения, которые дают минус первую степень переменной z: .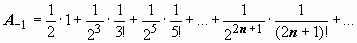

Легко сообразить, что это ряд для sh z при 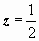, т.е. 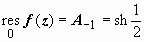, и .

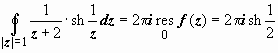Бесконечно удалённая особая точка. Будем считать точку z = ∞ особой точкой любой аналитической функции. В разделе Окрестности точек плоскости мы определили окрестности этой точки как внешности кругов с центром в начале координат: U (∞, ε) = { z ∈ | | z | > ε}. Точка z = ∞ является изолированной особой точкой аналитической функции w = f (z), если в некоторой окрестности этой точки нет других особых точек этой функции. Для определения типа этой особой точки сделаем замену переменной , при этом точка z = ∞ переходит в точку z ₁ = 0, функция w = f (z) примет вид . Типом особой точки z = ∞ функции w = f (z) будем называть тип особой точки z ₁ = 0 функции w = φ (z ₁). Если разложение функции w = f (z) по степеням z в окрестности точки z = ∞, т.е. при достаточно больших по модулю значениях z, имеет вид 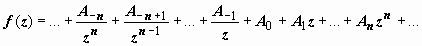, то, заменив z на , получим . Таким образом, при такой замене переменной главная и правильная части ряда Лорана меняются местами, и тип особой точки z = ∞ определяется количеством слагаемых в правильной части разложения функции в ряд Лорана по степеням z в окрестности точки z = 0. Поэтому
1. Точка z = ∞ - устранимая особая точка, если в этом разложении правильная часть отсутствует (за исключением, возможно, члена A ₀);
2. Точка z = ∞ - полюс n -го порядка, если правильная часть заканчивается слагаемым A _n · z ⁿ;
3. Точка z = ∞ - существенно особая точка, если правильная часть содержит бесконечно много членов.
При этом остаются справедливыми признаки типов особых точек по значению : если z = ∞ - устранимая особая точка, то этот предел существует и конечен, если z = ∞ - полюс, то этот предел бесконечен, если z = ∞ - существенно особая точка, то этот предел не существует (ни конечный, ни бесконечный).
Примеры: 1. f (z) = -5 + 3 z ² - z ⁶. Функция уже является многочленом по степеням z, старшая степень - шестая, поэтому z = ∞ - полюс шестого порядка.
Этот же результат можно получить по-другому. Заменим z на , тогда 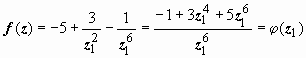. Для функции φ (z ₁) точка z ₁ = 0 - полюс шестого порядка, поэтому для f (z) точка z = ∞ - полюс шестого порядка.
2. . Для этой функции получить разложение по степеням z затруднительно, поэтому найдём : 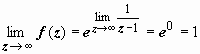; предел существует и конечен, поэтому точка z = ∞ - устранимая особая точка.
3. 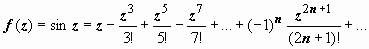. Правильная часть разложения по степеням z содержит бесконечно много слагаемых, поэтому z = ∞ - существенно особая точка. По другому этот факт можно установить исходя из того, что не существует.
Вычет функции в бесконечно удалённой особой точке. 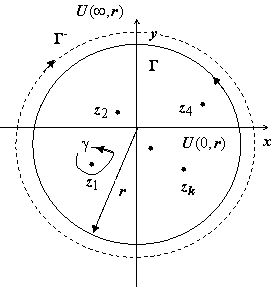Для конечной особой точки a 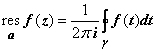, где γ - контур, не содержащий других, кроме a, особых точек, проходимый так, что область, им ограниченная и содержащая особую точку, остаётся слева (против часовой стрелке). Определим аналогичным образом: 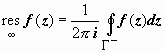, где Γ ⁻ - контур, ограничивающий такую окрестность U (∞, r) точки z = ∞, которая не содержит других особых точек, и проходимый так, что эта окрестность остаётся слева (т.е. по часовой стрелке). Таким образом, все остальные (конечные) особые точки функции должны находиться внутри контура Γ ⁻. Изменим направление обхода контура Γ ⁻: . По основной теореме о вычетах , где суммирование ведётся по всем конечным особым точкам. Поэтому, окончательно,

,

т.е. вычет в бесконечно удалённой особой точке равен сумме вычетов по всем конечным особым точкам, взятой с противоположным знаком. Как следствие, имеет место теорема о полной сумме вычетов: если функция w = f (z) аналитична всюду в плоскости С, за исключением конечного числа особых точек z ₁, z ₂, z ₃, …, z_k, то сумма вычетов во всех конечных особых точках и вычета в бесконечности равна нулю.
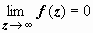Отметим, что если z = ∞ - устранимая особая точка, то вычет в ней может быть отличен от нуля. Так для функции , очевидно, ; z = 0 - единственная конечная особая точка этой функции, поэтому , несмотря на то, что , т.е. z = ∞ - устранимая особая точка.

Дата добавления: 2014-01-07