
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математическое описание волнового движения
|
|
|
|
Отвлечемся временно от описания строения атомов, чтобы познакомиться с математическим описанием волнового движения. Рассмотрим волну, изображенную на рисунке, которая с
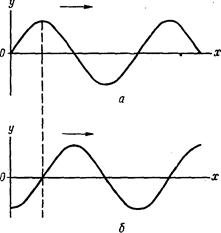
течением времени передвигается вдоль оси х в направлении, указанном стрелкой. Это волновое движение можно описать количественно с помощью дифференциального уравнения
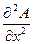 = (
= (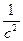 ) (
) (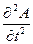 ),
),
где А — амплитуда, т. е. высота волны, измеряемая по оси у при данном расстоянии х; с — скорость, с которой передвигается волна, a t — время. Решением этого дифференциального уравнения является функция
A==аsin2p(х/l—nt).
где l — длина волны, n—ee частота и а—постоянная. Из уравнения можно найти амплитуду А во время t в положении х.
Другой тип волнового движения — стоячая волна — возникает при колебаниях струны с закрепленными концами. Стоячей волне отвечает стационарная картина с фиксированным профилем (вместо перемещающегося вдоль оси х, как в случае волны, изображенной ранее). Эмпирическим.путем
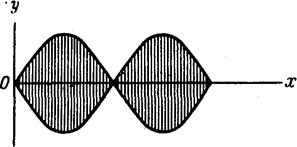
было найдено, что такая модель, обобщенная на случай трехмерной волны, лучше описывает поведение электрона, связанного с ядром. Дифференциальное уравнение, описывающее такую одномерную стоячую волну, имеет следующее решение:
A==2asin(2pх/l)cos2pnt,
или более просто
A=f(x)cos2pnt,
где f(x) — сокращенная запись для 2a sin(2px/l) — функция только координаты х.
Вторая производная функция по времени, будучи подставленной в уравнение, позволяет исключить величину t.
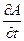 = -2a sin(2p
= -2a sin(2p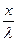 ) sin2pnt×2pn
) sin2pnt×2pn
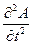 = -2a sin(2p
= -2a sin(2p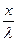 ) cos2pnt×4p2n2
) cos2pnt×4p2n2
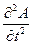 = -A4p2n2 n=
= -A4p2n2 n= 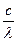
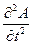 = -A
= -A = c2
= c2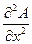
Получающееся уравнение для стоячей волны может быть обобщено для описания трехмерной волны:
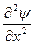 +
+ 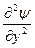 +
+ 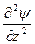 + 4p2y/l2 == 0,
+ 4p2y/l2 == 0,
где y—трехмерный аналог величины А). Введя сокращенное обозначение,
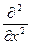 +
+ 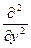 +
+ 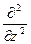 = Ñ2,
= Ñ2,
получаем
Ñ2y+4p2y/l2=0.)
Уравнения являются дифференциальными уравнениями, описывающими стационарную трехмерную волну, и не содержат переменной t. Целью исключения этой переменной было получение уравнения, решения которого не зависят от времени.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 316; Нарушение авторских прав?; Мы поможем в написании вашей работы!