Временная сложность алгоритмов

Временная сложность (ВС) – зависимость времени выполнения алгоритма от количества обрабатываемых входных данных. Здесь представляет интерес среднее и худшее время выполнения алгоритма. ВС можно установить с различной точностью. Наиболее точной оценкой является аналитическое выражение для функции: t=t(N), где t – время, N – количество входных данных (размерность). Данная функция называется функцией временной сложности (ФВС).

Например: t = 5N² + 3*2N + 1. Такая оценка может быть сделана только для конкретной реализации алгоритма и на практике обычно не требуется. Часто бывает достаточно определить лишь порядок функции временной сложности t(N).

Две функции f₁(N) и f₂(N) — одного порядка, если

Иначе это записывается в виде: f₁(N)= О (f₂(N)) (Читается " О большое ").

Примеры определения порядка ВС для некоторых алгоритмов:

1) Алгоритм линейного поиска. Этот алгоритм может быть использован как для упорядоченного, так и для неупорядоченного массива ключей. Работа алгоритма заключается в том, что при просмотре всего массива, начиная с первого и до последнего элемента, ключ из массива сравнивается с искомым ключом. Если результат сравнения положительный – ключ найден. Если же ни одно сравнение не выполнилось с положительным результатом, то ключа в массиве нет.

ФВС для алгоритма линейного поиска: t _{л. п.} = k₁ * N = O (N). Действительно, для отыскания ключа в худшем случае придется просмотреть все элементы массива. При этом время проверки каждого элемента одинаково и не зависит от конкретной вычислительной системы.

Оценим среднее время алгоритма, при этом будем исходить из следующего: пусть P_i – вероятность того, что будет осуществляться поиск элемента с ключом k_i; при этом предположим, что 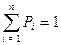, т.е. ключ со значением k_i не будет отсутствовать (в таблице обязательно есть элемент, поиск которого осуществляется). Среднее время (), как следует из алгоритма, пропорционально среднему числу операций сравнения () и равно ~=. Если ключи имеют одинаковую вероятность P₁=P₂=...P_N=P, а также учитывая, что, N*P=1, P=1/N, тогда ,

т.е. при линейном поиске в среднем необходимо просмотреть половину массива.

Рассмотрим упорядоченную таблицу, у которой элементы упорядочены по частоте обращений (по вероятности). Если имеем такую таблицу, то время – худшее: = О (N).

Распределение осуществляется по закону Зипфа: P_i = c / i, i = 1, 2, …, N, тогда ~=,

причем 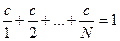, (N ® ¥)

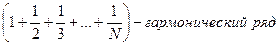, ln N – постоянная Эйлера.

Исходя из этого получили: с = 1 / ln N.

2) Алгоритм бинарного (двоичного) поиска. В словесной форме алгоритм двоичного поиска можно записать следующим образом:

1. Определить середину массива.

2. Если ключ, находящийся в середине массива, совпадает с искомым, поиск завершен.

3. Если ключ из середины массива больше искомого, применить двоичный поиск к первой половине массива.

4. Если ключ из середины массива меньше искомого, двоичный поиск необходимо применить ко второй половине массива.

5. Пункт 1-4 повторять, пока размер области поиска не уменьшается до нуля. Если это произойдет, то ключа в массиве нет.

ФВС для алгоритма бинарного поиска: t _{б. п.} = O (log ₂ N). Это объясняется тем, что на каждом шаге поиска вдвое уменьшается область поиска. До того, как она станет равной одному элементу, произойдет не более log ₂ N таких уменьшений, т.е. выполняется не более log ₂ N шагов алгоритма.

Изобразим графически функции ВС для линейного и двоичного поиска. Из графика видно, что для малых N нужно использовать линейный поиск, а для больших N — двоичный поиск.N_кр находятся в пределах 10.. 1000 в зависимости от характеристик используемого оборудования.

СД типа хеш-таблица.

СД типа хеш-таблица использует алгоритм поиска, основанный на идее хеширования. До сих пор, для поиска требуемой записи мы использовали организацию просмотра некоторого количества ключей. Очевидно, что эффективными алгоритмами поиска являются те, которые проходят это количество ключей при минимальном числе сравнений. В идеале хотелось бы иметь такую организацию таблицы, у которой не было бы ненужных сравнений, т.е. чтобы каждый ключ находился за одно сравнение, но в этом случае положение записи в таблице должно зависеть от значения ключа.

Операция включения элемента в таблицу.

Перед включением элемента в таблицу определяют его адрес с помощью хеш-функции: A = h(K), где K – ключ, а А – адрес элемента таблицы, причем 0 £ А £ N-1, т.е. хеш-функция – отображение множества ключей на множество адресов.

A = K mod N = (C₁ * k + C₂) mod N, где N – количество адресов в таблице.

“Хорошая” хеш-функция – это функция, которая быстро вычисляется и минимизирует количество коллизий. Коллизия – это ситуация, когда для разных ключей адрес один и тот же, т.е. h(k_i) = h(k_j), где i ¹ j. Минимизации можно добиться, если равномерно распределить элементы по адресному полю таблицы.

После вычисления адреса элемента таблицы есть две возможности размещения элемента:

1) поместить этот элемент по адресу, если адрес свободен;

2) если вычисленный адрес занят, то повторить хеширование, т.е. совершить рехеширование по следующей формуле: A1 = (A+C) mod N.

Таким образом, алгоритм включения элемента в таблицу будет иметь следующий вид:

1. Вычисление ключа с помощью хеш-функции. Если вычисленный адрес таблицы свободен, то помещаем в него элемент. Конец алгоритма.

2. Если вычисленный адрес таблицы занят, то перевычисляем адрес (проводим рехеширование) и переходим к п.1.

Чтобы процесс размещения элементов был равномерным, адресное поле таблицы делается больше множества ключей на 10-15%.

Операция исключения элемента из таблицы:

1. С помощью хеш-функции вычисляется предполагаемый адрес элемента таблицы.

2. Если по вычисленному адресу располагается искомый ключ, то запись найдена и ее удаляют. Конец алгоритма.

3. Если вычисленный адрес пуст, то элемента с заданным ключом в таблице нет. Конец алгоритма.

4. Если элемент таблицы содержит другой ключ, то перевычисляем (рехешируем) адрес и переходим к п.2.

Дата добавления: 2014-01-07