Применение бинарных деревьев в алгоритмах поиска

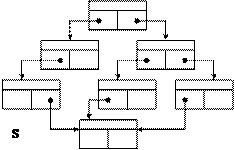
В односвязном списке невозможно использовать бинарные методы, они могут использоваться только в последовательной памяти. Однако, если использовать бинарные деревья, то в такой связной структуре можно получить алгоритм поиска со сложностью O(log ₂ N). Такое дерево реализуется следующим образом: для любого узла дерева с ключом T_i все ключи в левом поддереве должны быть меньше T_i, а в правом – больше T_i. В дереве поиска можно найти место каждого ключа, двигаясь, начиная от корня и переходя на левое или правое поддерево, в зависимости от значения его ключа. Из n элементов можно организовать бинарное дерево (идеально сбалансированное) с высотой не более чем log ₂ N, которое определяет количество операций сравнения при поиске.

Function Search (x: integer; t: ElPtr): ElPtr;

T_i L_Son R_Son

{поле Data заменим на поле Key}

var f: boolean;

begin

< T_i > T_i

f:=false;

while (t<>nil) and not f do

if x=t^. key then f:=true

else if x>t^. key then t:=t^. R_Son else t:=t^. L_Son;

Search:=t;

end;

Если получим, что значение функции = nil, то ключа со значением x в дереве не найдено.

	Функцию можно упростить, если организовать идею барьера, когда все листья указывают на введенный фиктивный элемент.

Function Search (x: integer; t: ElPtr): ElPtr;

begin

S^.key:=x;

while t^.key<>x do

if x > t^.key then then t:=t^. R_Son else t:=t^. L_Son;

Search:=t;

end;

Дата добавления: 2014-01-07