Представление графа в памяти ЭВМ

1) Графический способ представления (если граф небольшой).

2) Использование матриц. Матрица легко описывается и при анализе характеристик графа можно использовать алгоритмы линейной алгебры. Также используется представление графа в связной памяти, в том случае, если большее количество элементов в матрице равно нулю (матрица не заполнена).

Числовыми характеристиками графа являются: количество узлов, количество дуг, ранг графа. Ранг графа: R(G) = |X| - K, где К – количество компонентов связности графа в случае, если но не связан.

Рассмотрим матрицу смежности. Пусть задан граф G = (X, U), |X| = n. Имеем матрицу А размерности n ´ n, которая называется матрицей смежности, если элементы ее определяются следующим образом: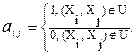

Рассмотрим применение матричной алгебры для определения характеристик графа. Выражение a _{i k} L a _{k j} означает, что между узлами i и j есть две дуги, проходящие через узел k, если значение выражения равно True.

Выражение 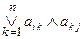означает, что всегда имеется путь между этими узлами длиною 2 (два), если выражение истинно.

А L А = А⁽²⁾ – логические операции заменяются арифметическими. Тогда каждый элемент a _{i j} будет давать информацию о том, есть ли путь из i в j (i, j = 1, 2,…,n).

Выражение А⁽ⁿ⁾ = А^{(n – 1)} L А означает, есть ли путь длиной n между различными узлами i. По диагонали будет характеристика, есть ли циклы (контура) в матрице.

Р = А V А⁽²⁾ V …V А⁽ⁿ⁾ = - матрица связности. Определяется, существует ли какой-либо путь между узлами i и j. Алгоритм вычисления данного выражения:

1. Р = А;

2. повторить 3, 4 (k=1, 2,…, n);

3. повторить 4 для i=1, 2, …,n;

4. повторить Р_{i j} = Р_{i j} V (Р_{i k} L Р_{k j}), j=1, 2,…, n.

В связной памяти наиболее часто представление графа осуществляется с помощью структур смежности. Для каждой вершины множества X задается множество М(X _i) соответственно вех его последователей (если это орграф) или соседей (для неорграфа). Таким образом, структура смежности графа G будет представлять собой список таких множеств: < М(X ₁), М(X ₂),…, М(X _n)> для всех его вершин.

Рассмотрим пример (узлы обозначаем в виде цифр: 1, 2,…, n):

			Для неорграфа: 1: 2, 3; 2: 1, 3; 3: 1, 2; 4: 5; 5: 4. Для орграфа: 1: 2; 2: 3; 3: 1; 4: 5; 5: -.

1 2 3 4 5

Структуру смежности можно реализовать массивом из n линейно связанных списков:

Представление графа может оказать влияние на эффективность алгоритма. Часто запись алгоритмов на графах задается в терминах вершин и дуг, независимо от представления графа. Например, алгоритм определения количества последователей вершин: C (X) X_i, S – количество дуг.

S = 0;

" x Î X выполнить:

начало

С(x)=0;

" t Î M(x) выполнить: C(x) = C(x) + 1;

S = S + C(x);

конец;

Дата добавления: 2014-01-07