Определение оптимальных решений на основе полученных уравнений регрессии

Проверка математической модели на адекватность

После дискриминации моделей и отбора из них лучшей производится проверка отобранной модели на адекватность. Указанная процедура производится с помощью следующего альтернативного соотношения:

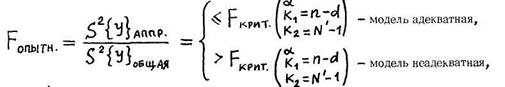
где N^’ — общее число опытов с учетом параллельных опытов. Общая дисперсия вычисляется по формуле

После дискриминации и проверки математической модели на адекватность, т.е. после получения математической модели, которая адекватно описывает изучаемое явление или процесс, приступают к решению основной задачи, т.е. к определению таких значений факторов, при которых функция отклика будет иметь наибольшее (или наименьшее) значение. Порядок решения указанной задачи проиллюстрируем на примере. Предположим, что после дискриминации и проверки на адекватность была получена математическая модель следующего вида

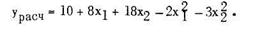
Требуется определить значения факторов Х₁ и Х₂, при которых функция отклика будет иметь наибольшее значение.

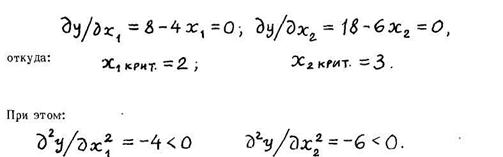
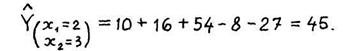
Решение. Дифференцируя функцию у _расч по переменным Х₁ и Х₂ _ и приравнивая производные нулю, получаем:

Следовательно, в критической точке функция отклика имеет максимум, равный:

С помощью уравнений регрессии представляется возможность не только определять экстремальные значения аргументов, при которых функция отклика имеет максимальное или минимальное значение, но и решать следующие задачи:

—ранжировать факторы по их влиянию на функцию отклика;

—прогнозировать развитие явления или процесса во времени, и, следовательно, решить вопрос об оптимальном управлении.

Дата добавления: 2014-01-07