Способы определения вероятностей состояний системы, описываемой случайным марковским процессом с дискретными состояниями и дискретным временем

Известны два способа: алгебраический и с помощью реккурентной формулы.

1. Алгебраический способ.

Сущность алгебраического способа проиллюстрируем на примереоднородной марковской цепи.

Пример 2. Рассматривается техническое устройство, которое может находиться в двух состояниях: исправно и неисправно. Вектор начального состояния системы Р _сост. и матрица вероятностей перехода системы Р_ij,.составляют:

;

Требуется построить размеченный граф перехода системы и вычислить вероятности состояний системы после одного, двух и трех шагов (К = 0, 1, 2 и 3).

Решение.

1. Строим размеченный граф перехода системы (рис. 2).

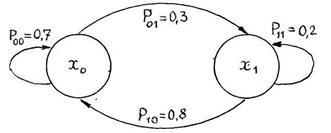
Рис. 2. Размеченный график марковского случайного процесса с дискретными состояниями и дискретным временем

2. Находим вероятности состояний системы после первого шага. Очевидно, что вектор состояний системы после первого шага (К = 1) изменится и станет равным

.

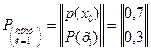при этом, поскольку процесс однородный, постольку матрица перехода системы из сотояния в состояние останется неизменной.

3. Определяем вероятности состояний системы после второго шага (К= 2).

Поскольку неизвестно, в каком состоянии система находилась после первого шага, постольку при определении вероятности состояний системы после двух шагов необходимо применить формулу полной вероятности. Например, вероятность того, что после двух шагов система будет находиться в состоянии Х_о, запишется так:

,

где — вероятность гипотезы о том, что после первого шага система была в состоянии Х₀;

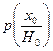— условная вероятность события, состоящего в том, что за время второго шага система останется в состоянии Х_о(P₀₀);

- вероятность гипотезы о том, что после первого шага система была в состоянии Х₁;

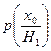— условная вероятность события, состоящего в том, что за время второго шага система перейдет из состояния Х₁. в состояние Х₀(P₁₀).

Подставляя для рассматриваемого примера численные значения вероятностей

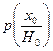=0,7; P₀₀=0,7; 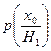= 0,3 и P₁₀=0,8; в формулу полной вероятности, получаем:

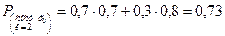
Естественно, что вероятность противоположного события, равна

= 1 - = 1 – 0,73 = 0,27.

Таким образом, вектор состояний системы после двух шагов запишется так:

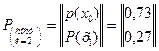
Аналогично по формуле полной вероятности определяются вероятности состояний системы после трех шагов, например, вероятность

и значить, вектор состояний системы после трех шагов имеет вид:

.

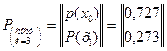Аналогично после четырех и более числа шагов.

Для установившегося режима получаем:

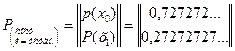
2. Определение вероятностей состояний системы после «К» шагов с помощью рекуррентной формулы

Вероятности состояний системы с дискретными состояниями и дискретным временем могут определяться не только с помощью алгебраического способа, но и с помощью рекуррентной формулы, представляющей собой матричное уравнение (произведение двух матриц, называемое уравнением Чепмена—Колмогорова)

,

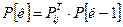где — вектор состояний системы после К шагов;

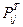— транспонированная матрица вероятностей перехода;

— вектор состояний системы после К-1 шагов.

Применяя указанную формулу для рассматриваемого примера, получаем:

после К=1 шагов:

;

после К=2 шагов: ;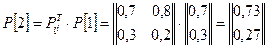

после К=3 шагов: ;

после n шагов: , что совпадает с решением алгебраическим способом.

Дата добавления: 2014-01-07