Вероятностный смысл энтропии

В изолированной системе, как уже говорилось, энтропия возрастает, если происходящие в системе процессы являются необратимыми. С позиции статистической физики, процесс является обратимым, если вероятности осуществления прямого и обратного процессов соизмеримы. Если же обратный процесс маловероятен, то прямой процесс является необратимым. Примером такого процесса является расширение газа в пустоту (самопроизвольное сжатие газа маловероятно).

Энтропия связана с так называемой термодинамический вероятностью.

Термодинамической вероятностью системы 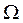называется число различных микросостояний системы, реализующих данное макросостояние.

Пример: № молекулы в сосуде

Вероятность процесса будет тем выше, чем больше в результате его существования возрастёт вероятность состояния системы 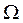(термодинамическая вероятность).

Число микросостояний, которое соответствует некоторому молярному объёму газа 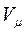, может быть определено как N_i, тогда термодинамическая вероятность первого состояния определяется выражением

(5.6.1)

где – число микросостояний, 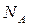– число Авогадро (т.е. число атомов находящихся в этих состояниях).

Воспользуемся формулой Стирлинга

(5.6.2)

И соответственно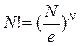

получим соотношение термодинамических вероятностей для двух различных объёмов газа и (N_A! Сократится, и будем будем считать газ не очень сжатым (т.е. 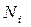» 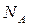))), тогда:

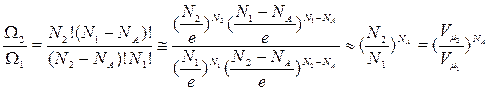
(5.6.3)

С другой стороны, в соответствии с первым началом термодинамики, разделим соотношение 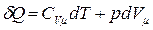на T и получим

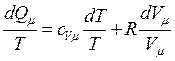
(5.6.4)

(5.6.5)

Для обратимого изотермического процесса 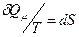, и все изменения состояния обусловлены изменением объёма. Тогда и

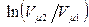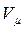Но может быть рассчитан, исходя из статистических соображений. Логарифмируя соотношение (5.6.3), связывающее и , получим

, или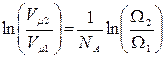

Отсюда

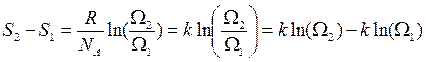
(5.6.6)

Таким образом, энтропию можно определить (с точностью до константы) в виде

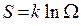. (5.6.7)

Это - формула Больцмана. Она связывает энтропию с термодинамической вероятностью системы. Чем выше вероятность состояния системы, тем больше энтропия системы. Т.к. в изолированной системе , т.е. S возрастает (по крайней мере, не уменьшается), то это означает, что термодинамическая вероятность в такой системе тоже растёт.

Все процессы в изолированной системе протекают в сторону увеличения вероятности состояния системы.

Это статистическое толкование второго начала термодинамики.

Из статистики следует что, в относительно малых системах возможны флуктуации, которые могут приводить к кратковременному уменьшению энтропии. Таким образом, 2-е начало не содержит в себе абсолютного запрета убывания энтропии. Другое дело, что на практике для систем с очень большим числом частиц закон неубывания энтропии выполняется без исключений.

Дата добавления: 2014-01-07