Основные понятия неравновесной термодинамики. Локальная формулировка первого начала термодинамики

В классической термодинамике рассматривались квазиравновесные процессы, т.е. такие процессы, которые протекли настолько медленно (D t), что значения параметров состояния во всех частях системы успевали выравниваться за время 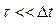, поэтому параметры состояния характеризовали всю систему в целом. Теперь будем анализировать поведение систем, которые не находятся в равновесном состоянии, то есть в них присутствуют потоки каких-либо величин, следовательно имеет место распределение и временная зависимость соответствующих параметров. В общем случае для описания системы нужно задавать термодинамические параметры как функции времени и радиус-вектора. Например, температуру, давление, концентрацию, плотность:

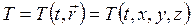
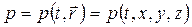
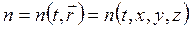(6.1.1)

.

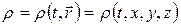Итак, температура изменяется от точки к точке. Но возможно ли определить температуру в точке? Поскольку температура определяется средней кинетической энергией молекул, точка, в которой определяется температура, не является математической. Под точкой при определении параметров системы подразумевается достаточно малый, но конечный объем .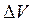

Для описания неравновесной системы ее нужно разбить на физически малые объемы, внутри каждого такого объема взять точку c координатами (x,y,z) и под параметром в этой точке, например, температурой, будем понимать значение температуры в физически малом объеме в окрестности этой точки.

Для описания квазиравновесных систем используются термодинамические функции: энергия, энтропия и другие. Для описания состояния неравновесных систем этих параметров недостаточно, для них удобно рассматривать плотности термодинамических функций. Плотность энергии (энергия единицы объема):

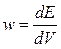; (6.1.2)

плотность энтропии (энтропия единицы объема):

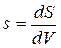. (6.1.3)

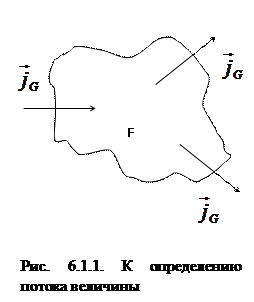В неравновесной системе может переноситься энергия, что характеризуется потоком. Напомним, что поток 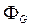переносимой величины G (рис. 6.1.1), определяется интегралом по поверхности F:

, (6.1.4)

где 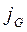- плотность потока величины .

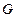В свою очередь под плотностью потока скалярной величины 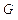понимают количество этой величины, которое проходит через единицу площади за единицу времени

Поток энергии 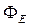через поверхность , очевидно, определится как интеграл

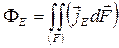. (6.1.5)

В выделенной подсистеме изменение энергии 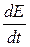может происходить, согласно закону сохранения энергии, только за счет отличного от нуля потока энергии извне и наружу. То есть изменение энергии выделенной подсистемы численно равно потоку через замкнутую поверхность, ограничивающую выбранную подсистему:

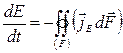. (6.1.6)

Здесь учитывается правило знаков, по которому вытекающий поток считается положительным, что приводит к уменьшению энергии выделенной подсистемы.

Выражение (6.1.6) представляет собой интегральную форму первого начала неравновесной термодинамики. Так как термодинамические параметры и функции зависят от координат, для анализа поведения неизолированных систем, являющихся подсистемами бóльших систем, необходимо иметь локальную формулировку законов.

Локальная формулировка первого начала неравновесной термодинамики имеет следующий вид

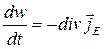. (6.1.9)

Локальная формулировка первого начала неравновесной термодинамики: Скорость изменения плотности энергии в каждой точке открытой системы равна дивергенции плотности потока энергии, взятой с обратным знаком.

Напомню определение дивергенции: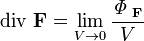

где Ф_F — поток векторного поля F через сферическую поверхность площадью S, ограничивающую объём V.

Необходимо отметить, что дифференциально малое изменение плотности энергии 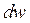можно представить в виде суммы двух компонент, одна из которых обусловлена процессами внутри системы 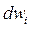, а вторая 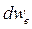– внешними факторами:

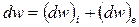. (6.1.10)

В том случае, когда речь идет о плотности энергии, первое слагаемое равно нулю и все приращение плотности потока энергии обусловлено внешними факторами.

Дата добавления: 2014-01-07