Амплитудная и фазовая частотные характеристики

Частотные характеристики описывают вынужден­ные движения системы, вызванные гармоническим воздействием на входе , где 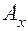– амплитуда; – угловая частота входных колебаний с периодом 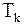. Если 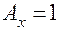, то входное воздей­ствие – единичное гармоническое.

По окончании переходного процесса на выходе линейной системы устанавливаются гармонические колебания 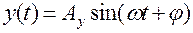той же частоты ω, но с другой амплитудой 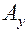и сдвинутые по фазе относительно входных колебаний на угол .

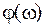Изменения амплитуды 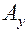и фазовый сдвиг 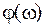являются функциями частоты ω и выражают динамические свойства системы. Если изменять частоту входных колебаний от 0 до ∞ и определять установившиеся амплитуду и фазу выходных колебаний для разных частот, можно получить зависимость соотношения амплитуд 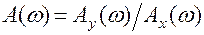от частоты – амплитудно–частотную (АЧХ) и сдвига фазы 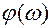– фазово–частотную (ФЧХ).

Проведение такого исследования можно представить, например, так (рис. 7.1): в трубопровод подачи топлива вмонтирована дроссельная заслонка, которую можно открывать и закрывать с определенной частотой при помощи специального механизма. При этом можно обеспечить синусоидальное изменение расхода топлива, являющегося входной величиной . Если измерять температуру в печи – выходной сигнал 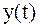, то увидим, что в установившемся режиме она будет изменяться с той же частотой, а максимумы и минимумы расхода и температуры будут сдвинуты по фазе (рис. 7.2).

Для каждой частоты входного сигнала (расхода газа) одной и той же амплитуды будут получены определенные амплитуда и фазовый сдвиг выходного сигнала (температуры в печи).

Если изобразить зависимость отношения амплитуд от частоты, получим амплитудно-частотную характеристику (рис. 7.3). Заметим, что у обычных инерционных звеньев АЧХ по мере увеличения частоты падает.

Хотя АЧХ теоретически продолжается до бесконечности, практическое значение имеет полоса пропускания, т.е. диапазон частот, в котором амплитуда колебаний выходного сигнала составляет не менее 5 % амплитуды колебаний максимума выходного сигнала. Если у АЧХ звена имеется максимум при , то соответствующую частоту называют резонансной.

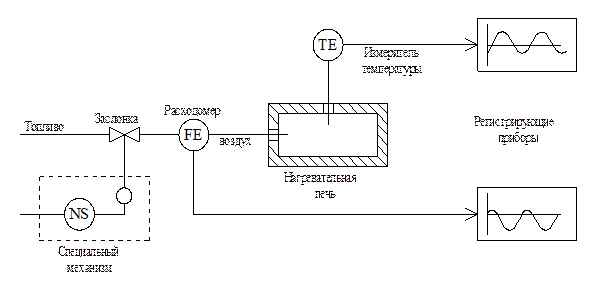
Рис. 7.1. Схема экспериментального определения частотных характеристик

Рис. 7.2. Входной и выходной сигналы в установившемся режиме

Изобразив на графике зависимость фазового сдвига от частоты (рис. 7.4), получим фазово–частотную характеристику. ФЧХ у обычных инерционных звеньев отрицательна, т.е. выходные колебания отстают по фазе от входных, причем это отставание увеличивается до полупериода с ростом частоты ω до бесконечности.

Рис. 7.3. Построение амплитудно-частотной характеристики (АЧХ)

Рис. 7.4. Построение фазовой частотной характеристики (ФЧХ)

Дата добавления: 2014-01-07