Тейлор (1685-1731) – английский математик

Формула Тейлора

Дифференциал сложной функции.

Инвариантная форма записи дифференциала

Пусть y = f(x), x = g(t), т.е. у - сложная функция. Тогда

dy = f¢(x)g¢(t)dt = f¢(x)dx.

Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какой- то другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.

Однако, если х - независимая переменная, то dx = Dx, но если х зависит от t, то Dх ¹ dx.

Таким образом, форма записи dy = f¢(x)Dx не является инвариантной.

Теорема Тейлора. 1) Пусть функция f(x) имеет в точке х = а и некоторой ее окрестности производные порядка до (n+1) включительно { т.е. и все предыдущие до порядка n функции и их производные непрерывны и дифференцируемы в этой окрестности}.

2) Пусть х- любое значение из этой окрестности, но х ¹ а. Тогда между точками х и а найдется такая точка e, что справедлива формула:

- это выражение называется формулой Тейлора, а выражение:

- называется остаточным членом в форме Лагранжа.

Доказательство. Представим функцию f(x) в виде некоторого многочлена P_n(x), значение которого в точке х = а равно значению функции f(x), а значения его производных равно значениям соответствующих производных функции в точке х = а.

(1)

Многочлен P_n(x) будет близок к функции f(x). Чем больше значение n, тем ближе значения многочлена к значениям функции, тем точнее он повторяет функцию. Представим этот многочлен с неопределенными пока коэффициентами:

(2)

Для нахождения неопределенных коэффициентов вычисляем производные многочлена в точке х = а и составляем систему уравнений:

(3)

Решение этой системы при х = а не вызывает затруднений, получаем:

…………………….

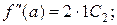
Подставляя полученные значения C_i в формулу (2), получаем:

.

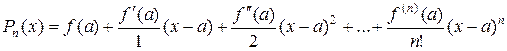Как было замечено выше, многочлен не точно совпадает с функцией f(x), т.е. отличается от нее на некоторую величину. Обозначим эту величину R_n+1(x). Тогда f(x) = P_n(x) + R_n+1(x). Теорема доказана.

Рассмотрим подробнее величину R_n+1(x). В точке х = а значение многочлена в точности совпадает со значением функции. Однако, при удалении от точки х = а расхождение значений увеличивается. Иногда используется другая запись для R_n+1(x). Т.к. точка eÎ(a, x), то найдется такое число q из интервала 0 < q < 1, что e = a + q(x – a). Тогда можно записать:

.

Тогда, если принять a = x₀, x – a = Dx, x = x₀ + Dx, формулу Тейлора можно записать в виде:

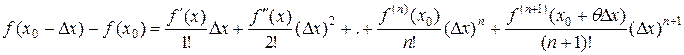где 0 < q < 1.

Если принять n =0, получим: f(x₀ + Dx) – f(x₀) = f¢(x₀ + qDx)×Dx – это выражение называется формулой Лагранжа. (Жозеф Луи Лагранж (1736-1813) французский математик и механик).

Формула Тейлора имеет огромное значение для различных математических преобразований. С ее помощью можно находить значения различных функций, интегрировать, решать дифференциальные уравнения и т.д.

При рассмотрении степенных рядов будет более подробно описаны некоторые особенности и условия разложения функции по формуле Тейлора.

Дата добавления: 2014-01-07