Точки экстремума. Определение 5.1. Функция f(x) имеет в точке х1 максимум, если ее значение в этой точке больше значений во всех точках некоторого интервала

Определение 5.1. Функция f(x) имеет в точке х₁ максимум, если ее значение в этой точке больше значений во всех точках некоторого интервала, содержащего точку х₁. Функция f(x) имеет в точке х₂ минимум, если f(x₂ +Dx) > f(x₂) при любом Dх (Dх может быть и отрицательным).

Очевидно, что функция, определенная на отрезке может иметь максимум и минимум только в точках, находящихся внутри этого отрезка. Нельзя также путать максимум и минимум функции с ее наибольшим и наименьшим значением на отрезке – это понятия принципиально различные.

Определение 5.2. Точки максимума и минимума функции называются точками экстремума.

Теорема. (необходимое условие существования экстремума) Если функция f(x) дифференцируема в точке х = х₁ и точка х₁ является точкой экстремума, то производная функции обращается в нуль в этой точке.

Доказательство. Предположим, что функция f(x) имеет в точке х = х₁ максимум. Тогда при достаточно малых положительных Dх>0 верно неравенство:

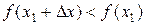, т.е.

Тогда

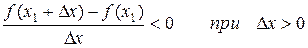
По определению: 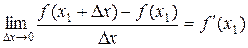. Т.е. если Dх®0, но Dх<0, то f¢(x₁) ³ 0, а если Dх®0, но Dх>0, то f¢(x₁) £ 0. А возможно это только в том случае, если при Dх®0 f¢(x₁) = 0. Для случая, если функция f(x) имеет в точке х₂ минимум теорема доказывается аналогично. Теорема доказана.

Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Красноречивый пример этого – функция у = х³, производная которой в точке х = 0 равна нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум.

Определение 5.2. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.

Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но этого недостаточно.

Пример 5.1. f(x) = ôxô; Пример 5.2. f(x) = .

y

x

В примере 5.1 в точке х = 0 функция имеет минимум, не имеет производной. В примере 5.2 в точке х = 0 функция не имеет ни максимума, ни минимума. Вообще говоря, функция f(x) может иметь экстремум в точках, где производная не существует или равна нулю.

Теорема. (Достаточные условия существования экстремума).

Пусть функция f(x) непрерывна в интервале (a, b), который содержит критическую точку х₁, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки х₁).

Если при переходе через точку х₁ слева направо производная функции f¢(x) меняет знак с “+” на “-“, то в точке х = х₁ функция f(x) имеет максимум, а если производная меняет знак с “-“ на “+”- то функция имеет минимум.

Доказательство. Пусть .

По теореме Лагранжа: f(x) – f(x₁) = f¢(e)(x – x₁),где x < e < x₁.

Тогда: 1) Если х < x₁, то e < x₁; f¢(e)>0; f¢(e)(x – x₁)<0, следовательно f(x) – f(x₁)<0 или f(x) < f(x₁).

2) Если х > x₁, то e > x₁ f¢(e)<0; f¢(e)(x – x₁)<0, следовательно

f(x) – f(x₁)<0 или f(x) < f(x₁).

Т. к. ответы совпадают, то можно сказать, что f(x) < f(x₁) в любых точках вблизи х₁, т.е. х₁ – точка максимума.

Доказательство теоремы для точки минимума производится аналогично. Теорема доказана.

На основе вышесказанного можно выработать единый порядок действий при нахождении наибольшего и наименьшего значения функции на отрезке:

1) Найти критические точки функции.

2) Найти значения функции в критических точках.

3) Найти значения функции на концах отрезка.

4) Выбрать среди полученных значений наибольшее и наименьшее.

Дата добавления: 2014-01-07