С закрепленными концами

Наиболее универсальным методом решения краевых задач математической физики является метод разделения переменных (метод Фурье). Основная идея метода состоит в сведении первоначальной краевой задачи к решению обыкновенных дифференциальных уравнений.

Приведем общую схему метода Фурье для решения однородного дифференциального уравнения в частных производных второго порядка с однородными граничными условиями, но неоднородными начальными. Решение этой задачи методом Фурье является основой для нахождения решения других, более общих краевых задач и проводится поэтапно в следующем порядке.

1. Сначала находят частные решения однородного дифференциального уравнения в частных производных, удовлетворяющие однородным граничным условиям. Для этого представляют частное решение в виде произведения функций, каждая из которых зависит только от одной из независимых переменных.

2. Подставляют частное решение в определяющее краевую задачу уравнение в частных производных. При этом задача нахождения частного решения редуцируется к решению отдельных обыкновенных дифференциальных уравнений.

3. Решают задачу Штурма – Лиувилля, то есть находят нетривиальное решение (собственные функции) однородных обыкновенных дифференциальных уравнений с однородными граничными условиями и определяют собственные значения. Иногда собственные функции и собственные значения определяются из условия периодичности или ограниченности искомого решения.

4. Находят решение оставшихся после решения задачи Штурма – Лиувилля обыкновенных дифференциальных уравнений, подчиняя их условиям ограниченности. На этом завершаются этапы нахождения частных решений.

5. Общее решение первоначальной краевой задачи представляют в виде суммы (ряда, интеграла) всевозможных частных решений.

6. Коэффициенты разложения искомого решения по собственным функциям краевой задачи определяют, удовлетворяя общее решение разложенным по собственным функциям начальным условиям поставленной задачи.

7. Показывают непрерывность полученного решения и возможность почленного двукратного дифференцирования функционального ряда (интеграла), определяющего решение краевой задачи.

В качестве примера применения метода разделения переменных рассмотрим задачу свободных колебаний конечной струны, закрепленной в точках и 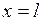. В математической постановке она состоит в решении волнового уравнения

, ,

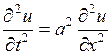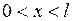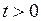
при выполнении граничных условий

, ,

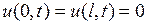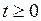и начальных условий

, .

По методу Фурье отличное от нуля частное решение сформулированной задачи ищется в виде

,

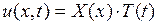где и 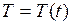– тождественно не равные нулю, дважды непрерывно дифференцируемые функции своих аргументов, подлежащие определению.

Подставляя это выражение в уравнение, получаем

,

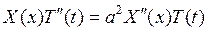откуда, разделяя переменные, находим

.

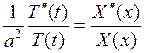Левая часть этого равенства зависит только от , а правая – только от . Поэтому, если, например, зафиксировать переменную , то отношение будет константой при любых . Наоборот, при фиксированном отношение 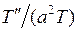также является константой при любом 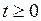. Из этого делаем вывод, что оба отношения являются постоянными при любых и 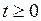, то есть равенство возможно лишь при

.

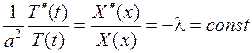Отсюда получаем систему обыкновенных дифференциальных уравнений

Из граничных условий имеем

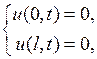
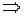
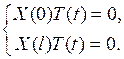
Поскольку ищется нетривиальное частное решение уравнения, то эти равенства возможны лишь при .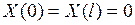

Таким образом, задача отыскания тривиально не равной нулю функции 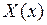сводится к следующей краевой задаче: найти нетривиальное решение дифференциального уравнения

,

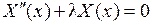удовлетворяющее однородным граничным условиям

.

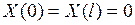Данная краевая задача называется задачей Штурма – Лиувилля. Числа называются собственными значениями этой задачи, а отвечающие этим нетривиальные решения 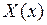– собственными функциями задачи Штурма – Лиувилля.

Найдем собственные значения и собственные функции задачи Штурма – Лиувилля. Рассмотрим три различных случая.

1. 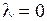. Из равенства 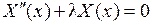получим уравнение 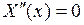. Составляем для него характеристическое уравнение . Его корни – действительные и кратные и, следовательно, общее решение уравнения (9.3.8) имеет вид 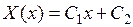, где и 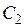– константы. Из граничных условий следует, что

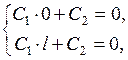
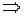
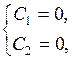
то есть 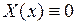. Поскольку ищутся нетривиальные решения задачи Штурма – Лиувилля, то ясно, что 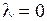не может служить собственным значением этой задачи.

2. . Характеристическое уравнение для уравнения 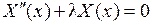имеет вид . Его корни , 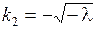– действительные и различные числа, и, следовательно, общим решением уравнения 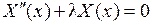является функция

.

Из граничных условий получаем

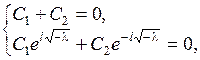
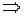
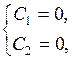
то есть при отличных от нуля решений задачи Штурма – Лиувилля не существует.

3. 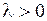. В этом случае характеристическое уравнение для 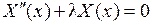имеет вид . Его корни 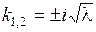– сопряженные комплексные числа, и общее решение уравнения 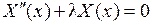записывается в виде

.

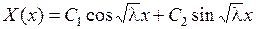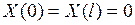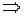
Из при получаем 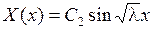. Второе граничное условие дает 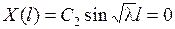. Если предположить, что , то снова получим решение 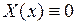. Поэтому должно быть

, .

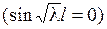
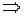
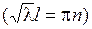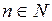Отсюда 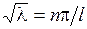, 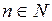. Таким образом, .

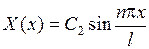Итак, если 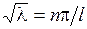, , 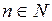то существуют нетривиальные решения задачи Штурма-Лиувилля. Обозначим через 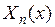решение, отвечающее фиксированному , а через – соответствующую постоянную, то есть

.

Система функций является системой собственных функций задачи Штурма – Лиувилля, отвечающих собственным значениям .

Для найдем решение первого уравнения системы, то есть уравнения

.

Его общим решением является функция

,

гд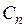е , – некоторые, пока неизвестные постоянные.

Тогда частным решением уравнения 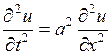является функция

,

где 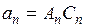, 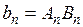– некоторые постоянные.

Вследствие линейности и однородности уравнения 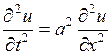сумма частных решений 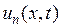так же является его решением, то есть функция

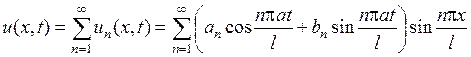
есть решение уравнения 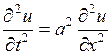, удовлетворяющее граничным условиям .

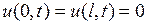Определим теперь и 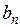так, чтобы решение удовлетворяло также начальным условиям , .

Предположим, что ряд сходится и его можно дважды почленно дифференцировать. Тогда из начальных условий будем иметь

,

.

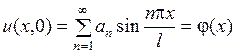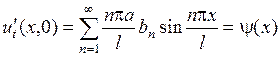Пусть функци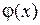и и разложимы в ряд Фурье по синусам на промежутке , то есть

, ,

, .

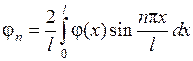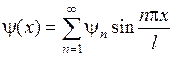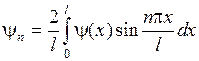Тогда для выполнения начальных условий надо положить 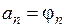, , 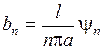то есть

, ,

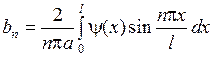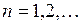
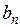Подставляя выражения для и в ряд

,

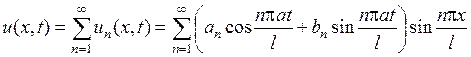найдем решение поставленной задачи.

Если ввести обозначения: , , 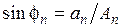, 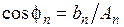то решение можно записать в виде

.

Каждый член этого ряда представляет собой так называемую стоячую волну, для которой точки струны совершают гармонические колебательные движения с амплитудой , фазой 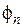и частотой .

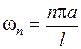Дата добавления: 2014-01-07