Булевы функции. Аппарат логики Буля, или иначе алгебры логики, оперирует с логическими переменными, которые могут принимать только два значения: 0 и 1

ЛОГИКА БУЛЯ

Аппарат логики Буля, или иначе алгебры логики, оперирует с логическими переменными, которые могут принимать только два значения: 0 и 1. Логические переменные определяют некую логическую зависимость, которую принято называть булевой функцией. Множество всех булевых функций и операций над ними образует булеву алгебру или алгебру логики. Булевы функции, или иначе функции алгебры логики (ФАЛ), могут принимать тоже только два взаимно исключающих значения 0 и 1. При формальном рассмотрении законов булевой алгебры логические переменные обычно обозначают строчными буквами латинского алфавита или присваивают им идентификаторы.

Логические величины 0 и 1 нельзя трактовать как числа, над ними нельзя производить арифметические действия, поскольку алгебра логики – это не алгебра чисел, а алгебра состояний. Тем не менее в булевой алгебре производятся логические действия над переменными, которые и определяют характер логических функций. Основные логические действия соответствуют простейшим операциям над множествами: инверсия, или отрицание, дизъюнкция, или логическое сложение, и конъюнкция, или логическое умножение. На основании этих трех логических действий строятся все сколь угодно сложные логические функции. При этом следует особо выделить функции одной и двух переменных, которые играют в алгебре Буля весьма важную роль. При помощи этих функций, используя принцип суперпозиции, можно описать любую логическую функцию любой сложности любого числа переменных.

Принцип суперпозиции заключается в том, что каждый аргумент логической функции может являться функцией других логических переменных, а именно: если есть функция f{ x ₁; x ₂; x ₃}, то возможно, что x ₁ = j (x ₄, x ₅).

Булевых функций одной переменной всего четыре.

1. Нулевая (const”0”) Ф = Х Ù=0 – значение функции равно нулю, каким бы ни было значение входной переменной.

2. Инверсия (не) Ф =– значение функции инверсно значению входной переменной.

3. Повторение (да) Ф = Х – значение функции повторяет значение входной переменной.

4. Единичная (const”1”) Ф = Х Ú= 1 – значение функции равно единице при любом значении входной переменной.

Из всех функций двух переменных десять являются самостоятельными и зависят как от переменной а, так и от переменной b. Притом функции Y₅,Y₆ отличаются от соответствующих им Y₇,Y₈ лишь порядком расположения аргументов. Таким образом, лишь восемь из 16-ти булевых функций двух переменных являются оригинальными.

1. Y₁ = a Ù b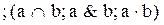– конъюнкция, логическое «и»;

2. Y₂ = a Ú b 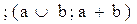– дизъюнкция, логическое «или»;

3. Y₃ = a / b 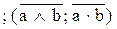– штрих Шеффера, логическое «и-не»;

4. Y₄ = a ¯ b – стрелка Пирса (функция Вебба), «или - не»;

5. Y₅ = a ¬b 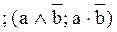– запрет b, «а, но не b»;

6. Y₆ = a ®b – импликация b, «если а, то b»;

7. Y₇ = b ¬a 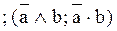– запрет а, «b, но не а»;

8. Y₈ = b ®a 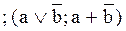– импликация а, «если b, то а»;

9. Y₉ = a º b – эквивалентность,

равнозначность;

10. Y₁₀ = a Å b 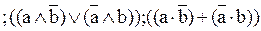– неравнозначность,

«сумма по модулю 2».

Дата добавления: 2014-01-07