Исчисление высказываний

ФОРМАЛЬНАЯ ЛОГИКА

Формальная математическая логика решает проблемы проверки правильности рассуждений в естественном языке, строя свои модели и правила их преобразования. Законы формальной логики, адекватные законам мышления человека для многих приложений, были разработаны еще Аристотелем. В результате конкретизации выводов формальной логики – новых полученных формул – мы можем оценить свойства исходных предложений и получить новые предложения естественного языка.

Из всего разнообразия естественного языка логика высказываний имеет дело только с узким кругом утверждений – повествовательных предложений, которым может быть приписано значение «истина» либо «ложь» (True и False). Каждое элементарное высказывание обозначается буквой. Кроме простейших высказываний, структура которых не анализируется (они поэтому называются атомами), вводится понятие сложного высказывания или формулы – комбинации более простых высказываний. Каждой формуле также можно приписать значение «истина» либо «ложь», и такое значение определяется на основе анализа логических операций между элементарными высказываниями.

Очевидно, что логика высказываний и теория булевых функций имеют теснейшую связь: обе эти модели являются булевыми алгебрами. Фактически, двоичные функции представляют собой функциональную модель логики высказываний, в которой атомные высказывания истолковываются как двоичные переменные. Истинностные значения истина и ложь в логике соответствуют 1 и 0 в модели двоичных функций, пара основных логических связок – отрицание и импликация – составляют базис, и все остальные производные логические связки соответствуют известным нам булевым функциям.

Тождественно истинная формула, т.е. такая формула, которая принимает значение 1 на всех интерпретациях ее элементов, называется тавтологией. Тождественно ложная формула, принимающая значение 0 на всех интерпретациях ее элементов, называется противоречием. Для указания того, что данная формула является тавтологией, используется знак |=, который помещается перед формулой, например: |=(А→В) (В→С) А→С. Для того чтобы проверить, является ли логическая формула тавтологией, можно составить таблицу истинности или привести к нормальной форме и использовать законы логики Буля.

Тавтологии или силлогизмы можно рассматривать как некоторые логические истинные схемы рассуждений, поэтому они играют роль законов логики высказываний. Впервые силлогизмы исследовались Аристотелем и имели фиксированную форму. Наиболее часто используемые из них следующие:

А→А – закон тождества;

А Ú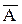– закон исключения третьего;

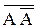– закон противоречия;

~ А – закон двойного отрицания;

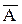→(А →В) – falso quodlibet (из ложного что угодно);

(А →В)А→В – закон отделения или modus ponens;

(А →В) 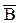→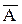– modus tollens (доказательство от противного);

(А →В) (В→С) →(А →С) – закон силлогизма;

(А →В) →(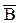→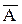) – закон контрапозиции.

Две формулы называются равносильными, если на всех наборах входных переменных они принимают одинаковые значения. Для обозначения отношения равносильности употребляют символ «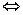», и равносильность или логическая эквивалентность формул А и В запишется как А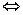В (на естественном языке это будет звучать так: «А тогда и только тогда, когда В»).

В логике высказываний все доказательства строятся на отношении порядка, т.е. на отношении, которое существует между причиной и следствием. При этом объектный символ импликации «→» заменяют на субъектный символ метаимпликации «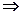». Говорят, что формула В является логическим следствием формулы А и пишут А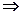В – «если А то В». Логическое следствие А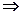В означает, что из истинности А следует истинность В, но если А ложно, то относительно В ничего утверждать нельзя. Между логическим следствием и логической эквивалентностью имеется связь, которая вытекает из соотношения

А ~ В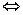(А→В)Ù(В→А).

Это соотношение означает: А ~ В, если и только если А→В и В→А.

Пусть А ~ В – тавтология, тогда А→В и В→А – тоже тавтологии, т.е. |= А ~ В, если и только если |= А→В и |= В→А.

Логическое следствие есть отношение порядка и удовлетворяет трем законам: - рефлексивности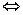: АА;

- антисимметричности: если А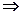В, то В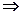А;

- транзитивности: если А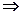В и В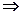С, то А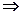С.

Вместо букв в логическое следствие можно поставить объектные высказывания, и тогда она наполнится конкретным содержанием, которое называется легендой.

Например: имеем А→В, А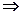В. Если принять, что А – сверкнула молния, В – грянул гром, то можно составить следующую легенду: «Известно, что если сверкнула молния, то грянет гром. Молния сверкнула, следовательно, должен грянуть гром».

Формализация процессов доказательств и выводов в логике высказываний имеет большое практическое значение и позволяет построить схемы доказательств, которые могут быть реализованы на ЭВМ. Доказательство здесь строится на отношении порядка, которое является общим случаем отношения эквивалентности. Логика высказываний является расширением логики Буля, поэтому все истинные тождества логики Буля автоматически становятся справедливыми логическими следствиями логики высказываний.

3.2. Предикаты и кванторы

С логической точки зрения двоичные объекты, что мы рассматривали в алгебре логики (булевой), – это высказывания, которые могут быть истинными или ложными. Формулы – это составные высказывания, истинность которых определяется истинностью входящих в них элементарных высказываний (А, В или С) и логическими операциями над этими элементарными высказываниями (инверсия, конъюнкция, дизъюнкция, импликация и т.д.).

Предикат – это функциональное высказывание. Логика предикатов – это расширение логики высказываний за счет использования предикатов в роли логических функций. Эти функции несколько отличаются от булевых функций. Булева функция однородна, т.е. для нее область значений функции и область изменения аргументов по типу одна и та же – логическая (либо истина, либо ложь). Для предикатов же область значений функции – логическая, а область изменения аргументов – предметная, отсюда следует вывод, что эта функция неоднородна.

Таким образом, принимающую одно из значений (0 или 1) функцию Р, аргументы которой могут принимать любое число значений из произвольного множества М, будем называть предикатом Р в предметной области М. Число аргументов предиката Р (х₁, х₂, …, х_n) называется его порядком.

Приведем примеры предикатных функций. Пусть имеется ряд простых высказываний:

P₁ = x₁ > A, P₂= x₂ > A, …, P_n = x_n > A.

Вместо высказываний P₁, P₂,…, P_n можно ввести одноместный предикат Р(х), для которого переменная х принимала бы значения из предметной области – х = { x₁, x₂,…, x_n }, а сама предикатная функция записалась бы так:

Р(х) = «х > A».

Теперь изменим исходный ряд высказываний на другой:

P₁ = x₁ > у₁, P₂= x₂ > у₂, …, P_n = x_n > у_n.

Здесь можно ввести уже двухместный предикат Р(х,у) = «x > у» с дополнительной предметной областью у = { у₁,, у₂,…, у_n }.

Введем трехместный предикат Р(х,у,z), который, допустим, означает, что «х есть сумма у и z». Если какой-нибудь переменной задать конкретное значение, скажем х = 5, то трехместный предикат превратится в двухместный Р(5, у, z) = Р¢(у, z) = «5 есть сумма у и z».

При х = 5 и у = 3 получим одноместный предикат:

Р(5, 3, z) = Р¢(3, z) = Р¢¢(z) = «5 есть сумма 3 и z».

Наконец, если добавить условие z = 2, то исходный предикат становится нульместным предикатом (константой или высказыванием), который в данном случае принимает истинное значение:

Р₁ =Р(5,3,2) = «5 есть сумма 3 и 2» = 1.

Но могло случиться, что z = 1, тогда имело бы место ложное высказывание: Р₀ =Р(5,3,1) = «5 есть сумма 3 и 1» = 0.

Таким образом, при замещении переменной х_i предметной постоянной а_i происходит превращение n-местного предиката Р(х₁, …, х _i, …, х_n) в (n – 1)-местный предикат Р(х₁, …, а _i, …, х_n). Приписав конкретные значения всем аргументам предикатной функции, мы тем самым получаем предикатную константу.

Функциональная природа предиката влечет за собой введение еще одного понятия – квантора. Пусть P(x) – предикат, определенный на некотором множестве «М». Высказывание: «для всех x Î M значение P(x) истинно» обозначается символом " х и называется квантором общности (“ All”). Другое высказывание: «существует хотя бы одно значение x Î M, при котором P(x) истинно» называется квантором существования и обозначается символом $ х (“Exist”). Выставляя кванторы перед предикатами, мы как бы усиливаем или ослабляем их действие.

С другой стороны, выражение " х P(x) = 1 означает, что конъюнкция всех значений предикатной функции равна 1:

" х P(x) = P(x₁) Ù P(x₂) Ù P(x₃) Ù ··· = 1.

Аналогично, квантор существования перед предикатом $ х P(x) = 1 означает, что дизъюнкция всех значений предикатной функции равна 1:

$ х P(x) = P(x₁) Ú P(x₂) Ú P(x₃) Ú ··· = 1.

Оба квантора можно выражать один через другой на основании закона де Моргана:

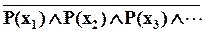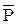P(x) == (x₁) Ú 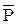(x₂) Ú 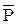(x₃) Ú =$ х 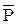(x),

$ х P(x) = 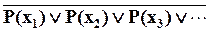= 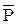(x₁) Ù 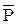(x₂) Ù 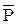(x₃) Ú·=" х 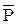(x).

Отсюда

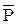(x) = $ х P(x) и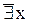 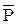(x) = " х P(x).

Переход от P(x) к " х P(x) или к $ х P(x) называется связыванием переменной x, а также навешиванием квантора на переменную x. Переменная, на которую навешивается квантор, называется связанной переменной; несвязанная переменная называется свободной. Свободная переменная – это обычная переменная, которая может принимать любые значения из множества М.

Если выражение P(x) – переменное высказывание, зависящее от значения x, то выражения " х P(x) или $ х P(x) не зависят от переменной x и при фиксированных значениях P и M превращают одноместный предикат в высказывание.

Навешивать кванторы можно и на многоместные предикаты, и вообще на любые логические выражения. Выражение, на которое навешивается квантор, называется областью действия квантора. Навешивание квантора на n-местный предикат уменьшает в нем число свободных переменных, превращая его в (n – 1)-местный предикат. Если на n-местный предикат навесить k кванторов, то он превращается в (n – k)-местный предикат.

Например, пусть P(x) = «x – четное число». Тогда высказывание " х P(x) истинно на любом множестве M четных чисел и ложно, если M содержит хотя бы одно нечетное число. Высказывание $ х P(x) истинно на любом множестве, содержащем хотя бы одно четное число, и ложно на любом множестве нечетных чисел.

Рассмотрим двухместный предикат P(x, y) = «x ≥ y» на множествах M. Навешивая квантор " х (x ≥ y), получаем одноместный предикат от y – «Для всех x из множества M высказывание «x ≥ y» – истинно. Если M – множество положительных чисел, то этот предикат истинен в единственной точке при y = 0. Если навесим предикат на вторую переменную " х "y(x ≥ y), то тогда истинность получим лишь на множестве, состоящем из одного элемента.

Основной задачей логики предикатов является установление истинности предикатных тождеств и логических следствий. Докажем, например, дистрибутивность квантора " х относительно конъюнкции и квантора $ х относительно дизъюнкции, т.е.

" х (Р₁(x) Ù Р₂(x)) = " х Р₁(x) Ù " х Р₂(x).

Пусть левая часть выражения истинна для некоторых Р₁ и Р₂, тогда для любого а Î M истинно Р₁(а) Ù Р₂(а), поэтому Р₁(а) и Р₂(а) одновременно истинны для любых а. Следовательно, правая часть выражения тоже истинна.

Если же левая часть ложна, то для некоторого а Î M ложно либо Р₁(а), либо Р₂(а), а следовательно, ложно либо " х Р₁(x), либо " х Р₂(x), то есть и правая часть ложна.

Аналогично доказывается тождество

$ х (Р₁(x) Ú Р₂(x)) = $ х Р₁(x) Ú $ х Р₂(x).

Однако, если квантор общности использовать совместно с дизъюнкцией, а квантор существования – с конъюнкцией, то будет иметь место логическое следствие

$ х (Р₁(x) Ù Р₂(x)) Þ $ х Р₁(x) Ù $ х Р₂(x).

И аналогично

" х (Р₁(x) Ú Р₂(x)) Þ " х Р₁(x) Ú " х Р₂(x).

Контрольные задания

1. Существует теорема геометрии о трех перпендикулярах: «Прямая, проведенная на плоскости перпендикулярно к проекции наклонной, перпендикулярна к самой наклонной». Эквивалентны ли этой теореме следующие утверждения (У1): «Прямая, проведенная на плоскости не перпендикулярно к наклонной, не перпендикулярна к ее проекции» и (У2): «Прямая, проведенная на плоскости перпендикулярно к наклонной, перпендикулярна к ее проекции».

Указание: Выделить в каждом высказывании более простые высказывания, а именно: пусть высказывание (А) будет: «Прямая на плоскости перпендикулярна наклонной», высказывание (В) будет: «Прямая перпендикулярна проекции наклонной». Тогда структуру сложных высказываний – теоремы и утверждений У1 и У2, – можно представить логическими формулами: АÞВ, 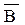Þ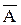и ВÞА. Для решения задачи теперь достаточно проверить эквивалентность соответствующих формул.

2. Предположим, что справедлива теорема: «Сеть Петри согласована и инвариантна только если она жива и ограничена». Как доказывать эту теорему? Определить, какие из следующих утверждений являются следствиями этой теоремы:

а) сеть Петри ограничена только в случае, если она инвариантна;

б) несогласованность сети Петри является достаточным условием отсутствия у нее живости и ограниченности;

в) если сеть Петри не согласована, то она не может быть неживой, но при этом ограниченной.

3. (Дело о рецидивистах). Трое рецидивистов, А, В и С, подозреваются в преступлении. Неопровержимо установлены следующие факты:

а) если А виновен, а В невиновен, то в деле участвовал С;

б) С никогда не действует в одиночку;

в) А никогда не ходит на дело вместе с С;

г) никто, кроме А, В и С, в преступлении не замешан, но по крайней
мере один из этой тройки виновен.

Можно ли на основании этих фактов выдвинуть обвинение против В? Против В или С? Против А?

4. Записать в форме предиката утверждения:

а) «Если два объекта из М обладают свойством Р, то они совпадают»;

б) «По крайней мере один студент решил все задачи»;

в) «Каждую задачу решил по крайней мере один студент».

5. Выразить с помощью предикатов следующие утверждения и их отрицания: а) «Один и только один объект обладает свойством Р»;

б) «По меньшей мере два объекта обладают свойством Р».

6. Выразить с помощью предикатов следующие утверждения:

a) все элементы массива b[j:k] нулевые.

b) ни один элемент массива b[j:k] не нулевой.

c) некоторые элементы массива b[j:k] нулевые.

d) все нулевые элементы массива b [0:n–1] находятся в b[j:k].

e) значения массива b [0:n–1] расположены в возрастающем порядке.

7. На множестве натуральных чисел определены предикаты: Р(х) = «число х делится на 8» и Q(x) = «х – четное число». Прочитайте следующие высказывания и выясните их истинность:

а) " хР(х); д) ;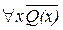

б) $ хР(х); е) " х(Р(х) ® Q(x));

в) " х Q(x); ж) " х (Q(x) ® Р(х));

г) 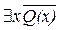; з) $ х(Q(x) ® Р(х)).

Дата добавления: 2014-01-07