Решение. Примеры решения задач

Примеры решения задач

1. Прямая бесконечная нить, равномерно заряженная электричеством с линейной плотностью t₁ =3×10^-7 Кл/м, и отрезок длиной l =20 см, равномерно заряженный электричеством с линейной плотностью t₂ =2×10^-7 Кл/м, расположены в одной плоскости перпендикулярно друг к другу на расстоянии r₀ = 10 см. Определить силу взаимодействия между ними.

В задаче рассматривается взаимодействие распределённых зарядов, поэтому для нахождения силы F следует воспользоваться соотношением:

. (1)

Нить создаёт вокруг себя электростатическое поле, в котором находится заряд, распределённый на отрезке длины l. Если выделить на этом отрезке малый участок длиной dr, то находящийся на нём заряд

dq = t₂dr (2)

можно считать точечным и рассматривать dF как силу, действующую со стороны электрического поля нити на dq. 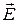– вектор напряжённости поля нити в месте нахождения электрического заряда dq. Электрическое поле равномерно заряженной нити определяется выражением

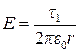. (3)

Выражение (1) можно переписать в скалярной форме, учитывая, что векторы 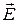и параллельны:

dF = Edq. (4)

Подставив (2) и (3) в (4), получим

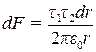. (5)

Для нахождения результирующей силы, действующей на отрезок нити с зарядом q₂ со стороны поля прямой бесконечной нити, проинтегрируем выражение (5) в пределах от r₀ до (r₀+l):

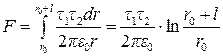. (6)

После подстановки числовых значений получим

.

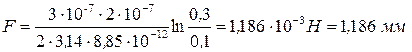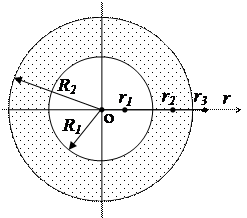
2. Полый стеклянный шар несёт равномерно распределённый по объёму заряд. Его объёмная плотность r =100 нКл/м³. Внутренний радиус шара R₁ =5 см, а наружный R₂ =10 см. Найти напряжённость электрического поля на расстоянии: а) r₁ =3 см; б) r₂ =6 см; в) r₃ =12 см от центра шара.

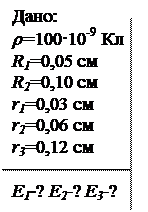Решение

Так как заряд шара распределён в пространстве симметрично относительно центра шара О, то и электрическое поле симметрично относительно этой точки. Это позволяет применить для решения задачи метод Гаусса. Из симметрии задачи следует, что вектор 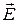направлен вдоль и зависит только от расстояния до центра шара r. Выберем гауссову поверхность в виде сферы, переменного радиуса r с центром в точке О. Учтем, что модуль напряжённости поля шара одинаков во всех точках этой поверхности и Е _n= E _r. Так как шар диэлектрический, следует применить теорему Гаусса для вектора электрического смещения 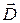. Тогда поток вектора смещения сквозь гауссову поверхность

,

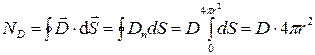где S – площадь гауссовой поверхности, r – её радиус.

Всё пространство можно разбить на 3 области:

1) 0 < r < R₁ 2) R₁ < r < R₂ 3) r > R₂. Применим теорему Гаусса для каждой области.

Для области 0 < r < R₁.

Величина свободного заряда, охватываемого поверхностью интегрирования в пределах первой области, равна нулю. Следовательно, поток вектора смещения также равен нулю, а так как площадь поверхности не нулевая, то смещение и напряжённость поля в пределах первой области равны нулю:

D₁ = 0, Е₁ = D/e₀ = 0.

Для области R₁ < r < R₂.

Свободный заряд, охватываемый гауссовой поверхностью, может быть выражен через объём той части шара, которая попала внутрь сферы радиусом r₂:

q _своб = 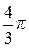(r₂³-R₁³)r.

Применяя теорему Гаусса, получим

D₂4pr₂² = ,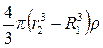

E₂ = =,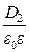

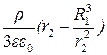где e – диэлектрическая проницаемость стекла.

В/м.

Для области r > R₂.

Внутрь поверхности попадёт весь заряд шара, поэтому

q _своб = (4/3)p(R₂³ - R₁³),

и, применив теорему Гаусса, получим выражение

D₃ 4pr₃² = (4/3) p (R₂³ - R₁³)r;

Е ₃ = D ₃/e₀ =;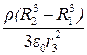

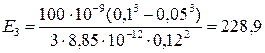В/м.

3. Тонкий стержень согнут в полукольцо. Стержень заряжен с линейной плотностью t =133 нКл/м. Какую работу нужно совершить, чтобы перенести заряд q =6,7нКл из центра полукольца в бесконечность?

Дата добавления: 2014-01-07