Алгоритм Кируса - Бека

Двумерное отсечение

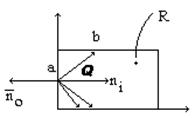
Есть область (видимая или невидимая) и через неё проходит отрезок.

Исходные данные: выпуклая область отсечения.

(рис. 1)

Алгоритм Кируса - Бека работает только с выпуклыми областями.

Используем понятие - внутренняя нормаль, т.е. если любая принадлежит ребру, b в другой границе окна, то произведение м.б. любым внутренним вектором на внутренней нормали, проведенной из этой же , будет положительно т.к. любой угол < 90⁰.

P2

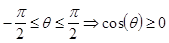(рис.2)

Если применить к внешней нормали, то . P1

Произведение вектора на внешнюю нормаль будет всегда отрицательным.

Пусть есть отрезок (P1, P2) (рис.2), представим его в параметрическом виде.

P(t) = P1 + (P2 - P1) t, где t - параметр (расстояние от начальной до конечной ) .

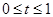Пусть какая-то точка F будет являться граничной точкой окна, тогда из вышесказанного мы можем сказать, что для отрезка (P1, P2) справедливо следующие:

1. П[ P(t) - F ] < 0, когда [ P(t) - F ] направлен во вне R.

2. n[ P(t) - F ] = 0 --

[ P(t) - F ] 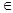плоскости, проходящей через точку F и перпендикулярной нормали.

3. n [ P(t) - F ] > 0, когда [ P(t) - F ] направлен во внутрь R.

Выводы:

1. Бесконечная прямая пересекает замкнутую выпуклую область ровно в двух точках и это справедливо для n - мерного пространства.

2. Пусть эти 2 точки 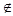одному ребру или граничной плоскости, тогда выражение n[ P(t) - F ] = 0 будет иметь только одно решение.

3. Если точка F 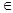ребру для которого вектор n внутренняя нормаль, то точка P(t) будет являться точкой пересечения данного отрезка с указанной граничной плоскостью.

Пример 1. Частично видимый отрезок.

(рис.3)

Уравнение прямой P1P2 = 0,2(X - 6).

Запишем этот отрезок в параметрическом виде т.е.:

P(1) = [-1, 1] + [10, 2] t = (10t - 1) i + (2t + 1) j, 0 <= t <= 1,

i, j - нормальные единичные вектора.

Зададим в окне нормали ,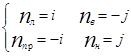

а) Для удобства вычисления допустим, что F = (0,0),

тогда [ P(t) - F ] = (10t - 1)i + (2t + 1)j.

Рассмотрим произведение n_л[ P(t) - F] = 10t - 1 = 0 t = 0,1.

Подставляем t в наше параметрическое уравнение,

т.е. P(0,1) = [-1,1] + [10,2] 0,1 = [0,1, 2].

б) Берем точку F = (8,4).

Опять находим вектор.

[ P(t) - F ] = (10t - 0)i + (2t - 3)j

n_n[ P(t) - i ] = 10t -8 = 0 t = 0,9

n_н[ P(t) - F ] = 2t + 1 = 0 t = - ½ - отвергаем

n_в[ P(t) - F ] = - (2t -3) = 0 t = 3/2 - отвергаем

Для n_н, n_в параметр t не лежит в заданной области. Эти точки t нам не нужны.

Подставляем t = 0,9 в параметрическое уравнение P(0,9) = [ 8, 2,8]

Отсюда , что видимый участок лежит в пределах. или

[0;1,2] ¸ [8;2,8].

Пример 2. Невидимый нетривиальный отрезок.

(рис. 4)

а) Допускаем, что пересекается с какой то стороной.

б) Перемножаем на все нормали.

в) Приравниваем n = 0.

г) Смотрим так это или не так.

Составляем параметрическое уравнение.

P(t) = [ 6, -2] + [ 4, 3]t

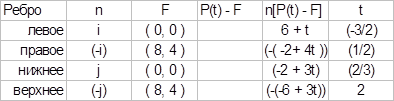
P₅P₆ не является тривиально невидимым.

л -3/2 = t; п 1/2 = t; н 2/3 = t; в 2 = t; - не верно => важна ориентация отрезка.

Если взять ориентацию отрезка P5 à P6, то получается что отрезок пересекает сначала правое, а затем нижнее ребро, но такого быть не может

такие параметры не подходят.

Из приведенного выше примера следует, что для правильного подбора параметров, нужно учитывать ориентацию отрезка.

Дата добавления: 2014-01-07