II.Дисперсия и среднее квадратическое отклонение непрерывной случайной величины

Дисперсия непрерывной случайной величины – это математическое ожидание квадрата отклонения случайной величины от ее математического ожидания

.

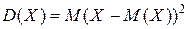Пусть Х – непрерывная случайная величина, возможные значения которой принадлежат отрезку [ a, b ], тогда дисперсия равна

.

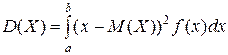Если возможные значения принадлежат всей оси x, то

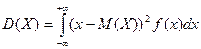
Для вычисления дисперсии непрерывной случайной величины более удобны формулы, следующие из теоремы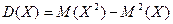

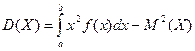или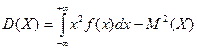

Среднее квадратичное отклонение непрерывной случайной величины

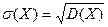
Свойства числовых характеристик дискретных случайных величин сохраняются и для непрерывных случайных величин.

Пример. 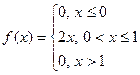. Найти M(X) и D(X).

Решение:

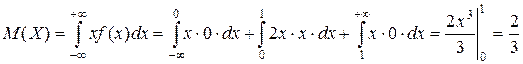
1-й способ:

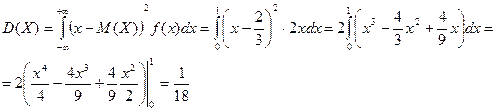
2-й способ: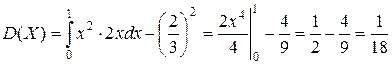

Дата добавления: 2014-01-07