
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
В этом случае конституенты покрываются следующими множествами
|
|
|
|
001 – P1=a
011 – P3=a+b
100 – P4=c
110 – P6=c+d
111 – P7=b+d
Из этого следует, что все возможные минимальные покрытия представляются множествам Р равным:
Р = а(а + b) с (с + d)(b + d)
Применяя, рассмотренные ранее, законы для операций над множествами:
Р = а(а + b) c (c + d)(b + d) = ac (b + d) = acb + acd
acb – { 0x1, 1x0, x11 }
acd – { 0x1, 1x0, 11x }
f 1 = 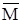 1M2 + M1
1M2 + M1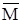 3 + M2M3
3 + M2M3
f 2 = 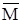 1M2 + M1
1M2 + M1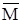 3 + M1M2
3 + M1M2
Рассмотрим более сложный пример.
Функция от четырех переменных:
| Kj | F |
Выпишем все образующие функцию конституенты, разбив на классы по количеству единиц.
0100 010x
0011 x100
0101 0x11
1001 x011
1100 01x1
0111 x101
1011 10x1
1101 1x01
110x
Объединяя их, получим: х10х х10х
| x10x | A | ||||||||
| 0x11 | B | ||||||||
| x011 | C | ||||||||
| 01x1 | D | ||||||||
| 10x1 | E | ||||||||
| 1x01 | F |
f 1 = M2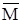 3 +
3 + 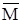 1M3M4 + M1
1M3M4 + M1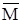 2M4
2M4
f 2 = M2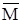 3 +
3 +  1M3M4 +
1M3M4 +  2M3 М4 + M1
2M3 М4 + M1 3M4
3M4
f 3 = M2 3 +
3 + 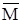 2M3M4 +
2M3M4 + 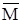 1М2 М4 + M1
1М2 М4 + M1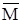 2M4
2M4
f 4 = M2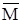 3 +
3 +  2M3M4 +
2M3M4 +  1М2 М4 + M1
1М2 М4 + M1 3M4
3M4
Получены тупиковые формы. Их сложность соответственно:
S1 = 8, S2 = 11, S3 = 11, S4 = 11
Следовательно имеем одну минимизированную форму f1
P = a(b+c)(a+d)(e+f)a(b+d)(c+e)(a+f) = a(b+c)(e+f)(b+d)(c+e) = a(b+cd)(e+cf) =
(ab+acd)(e+cf) = abe + abcf + acde + acdf
БУЛЕВА АЛГЕБРА
Алгебра – это множество М, с заданными на нем функциями, обладающими свойствами замкнутости.
f (mi) Î Mi; mi Î M.
Алгебра – некоторое множество М, с определенными на этом множестве операциями. Все функции,заданные на М,обозначаются буквой S –сигнатура алгебры. Множество М – носитель алгебры. Произв. алгебра А обозначается:
А < М, S >
ФУНДАМЕНТАЛЬНЫЕ АЛГЕБРЫ.
1. Алгебра А = < М, f0 >,где f0 - двуместная функция, называется группой. При этом f: a, b ® с, c = ab - обобщенное умножение
С обладает свойствами:
- если (а,b Î М, то результат обобщенного умножения так же принадлежит М
[(ab) Î M]
Это свойство замкнутости;
- (ab)c = a(bc) - свойство ассоциативности
- (ax) = b, ya = c - существованиеединственного решения уравнения
Группа, для которой выполнено условие:
ab = ba
называется коммутативной или абелевой группой.
ПРИМЕРЫ АЛГЕБРАИЧЕСКИХ СИСТЕМ
N - множество натуральных чисел
R - множество целых чисел
Z - множество действительных чисел
Определим алгебру вида:
А = < N, +, *, - >
Эта алгебра не является алгебраической системой
А = < N < +, *, > - алгебраическая система
Причем в данном примере содержится алфавит из бесконечного числа элементов.
Существуют алгебры с конечным алфавитом. Примером такой алгебры есть алгебра подстановок.
Образовывающаяся алгебра подстановок с помощью перестановок 3-х элементов х1, х2,х3.
Отметим возможные варианты.
| x1 | x2 | x3 | |
| x1 | x3 | x2 | |
| x3 | x2 | x1 | |
| x2 | x1 | x3 | |
| x2 | x3 | x1 | |
| x3 | x1 | x2 |
 Элементы носителя определяются следующим образом
Элементы носителя определяются следующим образом
a = x1 x2 x3 b = x1 x2 x3 c = x1 x2 x3
x1 x2 x3 x1 x3 x2 x2 x1 x3
d = x1 x2 x3 e = x1 x2 x3 c = x1 x2 x3
x2 x3 x1 x3 x1 x2 x3 x2 x1
Например элемент b означает,
что х1 переходит в х1
х2 переходит в х3
х3 переходит в х2
Определим групповую операцию, как общий переход:
 | |||
 | |||
bc = x1 x2 x3 x1 x2 x3 = x1 x2 x3 = d
x1 x3 x2 x2 x1 x3 x2 x3 x1
Составим мультипликативную таблицу:
| a | b | c | d | e | f | |
| a | a | b | c | d | e | f |
| b | c | a | d | c | f | e |
| c | c | e | a | f | b | d |
| d | d | f | b | e | a | c |
| e | e | c | f | a | d | b |
| f | f | d | e | b | c | a |
Проверим выполняется ли закон ассоциативности для данного примера:
(bd)f = cf =d
b(df) = bc =d
то есть, закон выполняется.
Так же можно показать, что закон справедлив для любых элементов данной алгебры.Видно, что алгебра замкнута, но не выполнено свойство коммутативности.
Поэтому алгебра – мультипликативная некоммутативная группа.
Алгебра вида
А = < М, *, + >
Называется кольцом, если < М, + > есть аддитивная абелевая группа, выполняется закон дистрибутивности.
Если операция обобщ. умн. кольца < М, * > содержит 1, то имеет место кольцо с единицей.
Если умн. коммут. то кольцо – коммутат. Полем называется кольцо с единицей, ненулевые элементы которого образуют группу по умножению. Если эта группа имеет конечное число элементов и является абелевой, то такие поля называются полями Галуа.
Рассмотрим примеры:
1.Множество действительных чисел с опер. слож. и умноженные есть коммутативное поле.
2. Алгебра вида:
А = < М, 0 , + >,где М {0,1,2,3,4,5} 0 , + по модулю 6.
Составим таблицу умножения и сложения.
с = а + в mod 6
| + | ||||||
с = ав mod 6
| * | ||||||
Из таблиц видно, что эта алгебра есть коммут. кольцо с 1.
3. А = < М, 0, + > М{0,1,2,3,4,5,6} c = a + b mod 7
| + | |||||||
| * | |||||||
Для данного алфавита можно определить и обратную операцию вычитания.
а – в = а(-в)
Для данной алгебры составленна таблица:
| а | -а |
По аналогии составляется таблица обратных элементов для деления.
1-1=1; 2-1=4; 3-1=5; 4-1=2; 5-1=3; 6-1=6;
Вышепреведенные алгебры являются полем Галуа.
СИСТЕМЫ УРАВНЕНИЙ И ПОЛЯ ГАЛУА.
 Как и в обычной алгебре можно решать системы уравнений и в полях Галуа.Возьмем следующую систему:
Как и в обычной алгебре можно решать системы уравнений и в полях Галуа.Возьмем следующую систему:
X1+3x2+6x3=2
4x1+5x2+2x3=1
2x2+x3=5
Будем решать систему по методу Гаусса:


1 3 6
 = 4 5 2 mod 7 = (5+48–4–12) mod 7=37 mod 7 = 2
= 4 5 2 mod 7 = (5+48–4–12) mod 7=37 mod 7 = 2
0 2 1


2 3 6
 1 = 1 5 2 mod 7 = (–109) mod 7=(140-109) mod 7 = 31 mod 7 = 3
1 = 1 5 2 mod 7 = (–109) mod 7=(140-109) mod 7 = 31 mod 7 = 3
0 2 1
 2 = 103 mod 7 = 5
2 = 103 mod 7 = 5  3 = (27-21) mod 7 = 0
3 = (27-21) mod 7 = 0
x1=3*2-1=3*4=5
x2=5*2-1=5*4=6
x1=0*2-1=0*4=Æ
5+3*6+6*Æ=5+4+Æ=2+Æ=2
4*5+5*6=6+2=1
2*6=5
БУЛЕВЫ АЛГЕБРЫ.
Изоморфизмом между алгебрами называется взаимооднозначное соответствие j между носителями и сигнатурами.
fi(x1,…xn) =xk Þ j (fi)[j (x1),…j (xn)] = j (xk)
Алгебры для которых существует изоморфизм j называют изоморф-ми.
Очевидно, что законы справедливые для некоторой алгебры, также будут справедливы и для изоморфной с ней алгебры.
Булевы алгебры – алгебры вида:
A = < M, +, *, - > для которых справедливы следующие отношения:
" хi Î M
1. xi + xj = xj + xi
2. xi * xj = xj * xi
3. (xi + xj) + xk = xi + (xj +xk)
4. (xi * xj) * xk = xi * (xj *xk)
5. (xi + xj) * xk = xi *xk+ xj*xk
6. xi + xj * xk = (xi + xj)(xi+xk)
7. xi+xj Î M, xi xj Î M
8. x E = x; xÆ = Æ; x + E = E; x + Æ = x;
9. x *  = E; x *
= E; x *  = Æ;
= Æ;
Множество вида М = {Ij, E, Æ}
Ij – интервалы пораждающих множеств;
E – единичное множество;
Æ - пустое множество;
и определенные на нем операции +, *, - есть булева алгебра или алгебра множеств. Булевы алгебры есть частный случай фундаментальных видов алгебр.
АЛГЕБРА БУЛЯ.
Булевой переменной является переменная, которая принимает значение 0 или 1. Будем обозначать такую переменную Х. Если в некоторой алгебре Буля определены функции от к переменных, то будем называть её к-значной, а сигнатуру обозначать как Рк .
Операция обобщ-го сложения в случае булевых алгебр называют дизъюнкцией, а операция обобщ-го умножения – конъюкцией.
Групповая операция обобщ. сложения:
х1 х2 ~ x1 + x2
х2 ~ x1 + x2
Операция обобщенного умножения:
x1&x2
0  0 = 0 0 & 0 = 0
0 = 0 0 & 0 = 0
0  1 = 1 0 & 1 = 0
1 = 1 0 & 1 = 0
1  0 = 1 1 & 0 = 0
0 = 1 1 & 0 = 0
1  1 = 1 1 & 1 = 1
1 = 1 1 & 1 = 1
Установим выполдняется ли для данной алгебры законы теории множеств:
1. Дистрибутивный закон
х1(х2 х3)=х1х2
х3)=х1х2 х1х3
х1х3
Составим таблицу:
| x1 | x2 | x3 | х1(х2 х3) х3)
| х1х2 х1х3 х1х3
|
1-й закон дистрибутивности применим к алгебре Буля. Аналогичная таблица для 2-го закона дистрибутивности.
(х1 х2) (х1
х2) (х1 х3) = x1
х3) = x1 (x2 & x3)
(x2 & x3)
| x1 | x2 | x3 | (х1 х2) (х1 х2) (х1 х3) х3)
| x1 (x2 & x3) (x2 & x3)
|
2. Проверим закон де Моргана.
Отрицание конъюкции есть дизъюнкция отрицания.

 1&
1&  2 =
2 =  1
1
 2
2
| x1 | x2 |   1& 1&  2 2
|  1 1  2 2
|
Отрицание дизъюнкции равно конъюкции отрицания.

 1
1
 2 =
2 =  1&
1& 2
2
| x1 | x2 |   1 1  2 2
|  1& 1& 2 2
|
Первый и второй законы де Моргана применимы для алгебры Буля.
ПРИОРИТЕТЫ АЛГЕБРЫ БУЛЯ.
1. –
2. &
3. Å
4. 
ОСНОВНЫЕ ОПЕРАЦИИ АЛГЕБРЫ БУЛЯ.
(АЛГЕБРЫ ЛОГИКИ).
ТАБЛИЦЫ ИСТИННОСТИ ЭТИХ ОПЕРАЦИЙ.
1. «НЕ» - х 
0 1
1 0
2. х1 х2 «ИЛИ»
х2 «ИЛИ»
| х1 х2 | х1 х2 х2
|
| 0 0 | |
| 0 1 | |
| 1 0 | |
| 1 1 |
3. Конъюкция х1& х2 «И»
| х1 х2 | х1& х2 |
| 0 0 | |
| 0 1 | |
| 1 0 | |
| 1 1 |
4. Импликация х1® х2 «ЕСЛИ ТО»
| х1 х2 | х1® х2 |
| 0 0 | |
| 0 1 | |
| 1 0 | |
| 1 1 |
5. Эквиваленция х1 ~ х2 «ТОГДА И ТОЛЬКО ТОГДА»
| х1 х2 | х1 ~ х2 |
| 0 0 | |
| 0 1 | |
| 1 0 | |
| 1 1 |
ПРЕДСТАВЛЕНИЕ ФУНКЦИИ В АЛГЕБРЕ БУЛЯ.
Функция трех переменных:
| x1 | x2 | x3 | f |
Кроме табличного задания алгебры логики применяются различные аналитические методы. К ним относятся – дизъюктивная и коньюктивная форма. Для представления в дизъюктивной соверш. норм. форме (ДСНФ) вводится фар-кая функция единицы, которая соответствует конституентам, в которых функция принимает значение = 1.
Единичная функция записывается,как элементарная конъюнкция, содержащая n – переменных и называется минитермом. Алгоритм представления функции алгебры логики в виде ДСНФ записывается в виде:
1) Выбрать в таблице функции все наборы аргументов, на которых функция обращ. в единицу
2) Вычислить конъюкцию, соответствующей этим наборам аргументам. При этом аргумент xi входит в данный набор как 1, он вписывается без изменения в конъюнкцию, соответствующую данному набору. Если хi входит как 0,то в конъюнкцию вписывается его отриц.
3) Все полученные конъюнкции соединены между собой знаками дизъюнкции.
Для примера запишем ДСНФ
f(х1,х2, х3) =  1
1  2
2  3
3 
 1 x2
1 x2  3
3 
 1
1  2 x3
2 x3  x1
x1  2
2  3
3  x1
x1  2 x3
2 x3 
 x1 x2
x1 x2  3
3
Для представления функции алгебры логики в КСНФ вводится хар-кая
функция О,которая соответствует набору, на котором функция принимает значение О. Функция нуля записывается как элементарная дизъюнкция, содержащая n-переменных и называется макситермом.
Алгоритм построения КСНФ:
1) Выбрать в таблице функции все наборы аргументов, на которых функция обращается в О.
2) Выписать дизъюнкции, соответствующие этим наборам. При этом если хi входит как О, он вписывается без изменений в дизъюнкцию, если хi входит как 1, то в дизъюнкцию вписывается его отрицание.
Для примера запишем КНФ
f(х1,х2, х3) = (x1  x2
x2
 3) & (
3) & ( 1
1
 2
2 
 3)
3)
По аналогии с теорией множеств при минимизации:
ДСНФ ® ДНФ
КСНФ ® КНФ
ДНФ,КНФ – обозначения для сокращения макситермами и минитермами. Номера мини- и макситермов являются дес-ными экв-ми соответствующего набора, на котором функция принимает 1 или 0 соответственно, то есть
(ДСНФ) f(х1,х2,х3) = m0  m2
m2  m3
m3  m4
m4  m5
m5  m6
m6
(КСНФ) f(х1,х2,х3) = m1 & m7
Согласно теореме Шеннона функция в ДСНФ имеет вид:
f(х1,…,хk) =  f(d1,…,dk) & x1d1* x2d2… xkdk
f(d1,…,dk) & x1d1* x2d2… xkdk
Функция трех переменных задана таблично:
| x1 | x2 | x3 | f |
f(х1,х2, х3) =  1
1  2
2  3
3 
 1 x2
1 x2  3
3 
 1x2 x3
1x2 x3  x1 x2 x3 (ДСНФ)
x1 x2 x3 (ДСНФ)
Выясним каково количество возможных булевых функций к-значных.
Если мы имеем к переменных, то из них можно составить m=2к комбинаций, а так как для каждой комбинации может быть задана своя функция, то общее число возможных функций V=2m=22^k
Теорема:
Алгебра множеств с к-порожденными множествами изоморфна к-значной алгебре Буля.
Доказательство:
Изоморфизм строится следующим образом:
j (Мi)=xi - для алгебры множеств
j (fi)=yi - для алгебры Буля
Тогда согласно представлению Булевых функций в ДСНФ и представлению функций от порождающих множеств в СНФК следует следующее:
fj(Mi) = 
 Mvdv ;
Mvdv ;
yj(xi) = 
 xvdv ;
xvdv ;
Основным следствием этой теоремы является возможность применения всех методов минимизации из теории множеств для алгебры Буля.
Метод Квайна для функции Буля:
0 0 0
0 1 0 0х0
0 1 1 х11
1 1 1
Строим таблицу Квайна:
| 0х0 | ||||
| х11 |
Y(x1, x2, x3) =  1
1 3
3 x2x3
x2x3
Минимизация по методу Карно:
 х1 х2х3 х1 х2х3
| ||||
f(x1, x2, x3) =  1
1 3
3 x2x3
x2x3
ФУНКЦИОНАЛЬНО ПОЛНЫЕ СИСТЕМЫ ФУНКЦИЙ.
Запишем таблицу функций 1-й перем.:
| x | y1 | y2 | y3 | y4 |
y1 – функция константы О;
y2 – переменная х;
y3 – отриц. переменная х;
y4 – конст-ты 1.
Для алгебры с двузначной логикой составим аналогичную таблицу всех возможных функций.
| х1 | х2 | F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | F15 |
Некоторые из этих функций встречались ранее:
F1(x1, x2) = x1 * x2 - дизъюнкция
F6(x1, x2) = x1 Å x2 - слож. по модулю 2
F7(x1, x2) = x1  x2 - конъюкция
x2 - конъюкция
Сведем в таблицу:
| Функция | Название | Предназначение |
| F0 | конст-та 0 | Æ |
| F1 | конъюкция | Логич. умнож. х1х2 |
| F2 | отрицание по х2 | х1  2 2
|
| F3 | повт-ль х1 | х1 |
| F4 | запрещение по х1 |  1х2 1х2
|
| F5 | повт-ль х2 | х 2 |
| F6 | сумма по mod 2 | х1Åх2 |
| F7 | дизъюнкция | логич. сложен. х1 х2 х2
|
| F8 | стрелка Пирса | х1 ¯ х2 |
| F9 | эквив-ти | х1 ~х2 |
| F10 | отрицание х2 |  2 2
|
| F11 | импликация по х2 | х2®x1 |
| F12 | отрицание х1 |  1 1
|
| F13 | импликация по х1 | x1 ® х2 |
| F14 | отр. конъюкции |  1 1  2 2
|
| F15 | конст-та 1 |
Функционально-полной системой алгебры Буля – набор функций Рк, с помощью которых может быть выраженна любая функция из Рк.
Тривиальной функционально-полной системой является весь набор функций из Рк.
Базисом алгебры Буля называется функционально-полная система, которая перестает быть таковой при выбрасывании из неё любой функции.
Примером алгебры с функционально-полной системой, но не являющейся базисом является функция вида:
А = < M,  , &, - >
, &, - >
На основании законов де Моргана из неё можно получить алгебры с базисами.
А1 = < M,  , - >, А2 = < M, &, - >
, - >, А2 = < M, &, - >
Принцип нахождения функционально-полных систем и базисов для Рк.
Будем искать такой набор из Рк, с помощью которого можно представить функции дезъюнкции, конъюкции, отрицания, а следовательно и все остальные функции. Для изучения свойств пространства Р2, т. е. Функция от двух переменных, представим все функции с помощью операций дезъюнкции, конъюкции и отрицания.
| F1 = х1*х2 |
F2 = х1* 2 2
|
F4 =  1*х2 1*х2
|
F6 = х1Åх2 =  1*х2 1*х2 х1* х1* 2 2
|
F7 = х1  х2 х2
|
 F8 = F8 =  1* 1* 2 = 2 =  1 1  2 2
|
 F9 = F9 =  1 1 2 2  х1х2 = х1Åх2 х1х2 = х1Åх2
|
F10 =  2 2
|
F11 =  1 1 2 2  х1 х1 2 2  х1х2 = x1 х1х2 = x1  2 2
|
F12 =  1 1
|
F13 =  1
1 2
2 
 1х2
1х2  х1х2 =
х1х2 =  1
1  х2
х2
F14 =  1
1 2
2 
 1х2
1х2  х1
х1 2 =
2 =  1
1 
 2 =
2 =  1
1 2
2
Для каждой из перечисленных функций существует двух ходовой логический элемент.
Изобразим эти элементы.
F1 = x1x2 F2 = x1 2 F4 =
2 F4 =  1x2
1x2
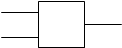

 x1 x1 x1
x1 x1 x1
x2 & y1 x2 & y2 x2 & y4
 F6 = х1Åх2 F7 = х1
F6 = х1Åх2 F7 = х1  х2 F8 =
х2 F8 =  1
1
 2
2


 x1 x1 x1
x1 x1 x1
x2  y6 x2 1 y7 x2 1 y8
y6 x2 1 y7 x2 1 y8
 F9 = х1Åх2 F10 =
F9 = х1Åх2 F10 =  2 F11 = x1
2 F11 = x1
 2
2


 x1 x1 x1
x1 x1 x1
x2  y9 x2 1 y10 x2 1 y11
y9 x2 1 y10 x2 1 y11
F12 =  1 F13 =
1 F13 = 1
1  х2 F14 =
х2 F14 =  1
1 2
2





 x1 x1 x1
x1 x1 x1
 x2 1 y12 x2 1 y13 x2 & y14
x2 1 y12 x2 1 y13 x2 & y14
На основании этих элементов можно синтезировать любую логическую функцию.
f(х1,х2,х3) = х1х2х3 
 1х2
1х2  х1
х1  2
2 
 1
1 2
2 3
3
 02 07
02 07
x1 00 1
x2 01 & 03 04 12
04 05 09 1
x3 02 & 06 & 08 09 1 14 f
00 1 07 &
05 10 10
01 01 & 11 1
1 00
& 11
06
Реализуем функцию вида f(х1,х2,х3):
 | |||||
 |  |
f(х1,х2,х3) = х1 2х3 &
2х3 &  1х3
1х3

x1 00 04
x2 01 & 03 04 1 06
x3 02 & 04
& 08 1 f 09
05 07
& 05 05 1
 |  |
f(х1,х2,х3) = х1 2х3
2х3 
 1х3 =
1х3 =  1
1 х2
х2
 3
3 x1
x1
 3
3
 x1 00 00
x1 00 00
x2 01 00 1 03 03 1 05
x3 02 01
04 1 06
08
02 00 1 10 f
02 1 04 04 1 07 1 09
СВОЙСТВА БУЛЕВЫХ ФУНКЦИЙ.
Функциональным классом называется множество всех функций, обладающих определенным свойством.
Функциональный класс замкнутый,если суперпозиция этого класса принадлежит этому же классу.
Например, класс функций, полученных с помощью дизъюнкции аргументов замкнут.
y(x1,x2) = x1 x2 ,где x2(z1,z2) = z1
x2 ,где x2(z1,z2) = z1 z2
z2
y(x1,x2(z1,z2)) = y(x1,z1,z2) = x1 z1
z1 z2
z2
Перечислим некоторые свойства. Для булевой функции определим понятие набора.
Набор – фиксируемое значение аргументов функции d, t d = {0110}
Между различными наборами установим соотн. сравнения:
d1 > d2, если любой элемент набора d1 ³ соответственно элементу из набора d2
d1 = (11010)
d2 = (01010) Þ d1 > d2
t1 = (01001)
t2 = (10100) Þ 2 набора несравнимы
d = (d1, d2, …,dn)
t = (t1, t2, …,tn) наборы знач. перем. знач. и считается d > t, если di > ti
ТЕОРЕМА.
Если булева функция может быть представлена в нормальной дизъюктивной форме без отрицания, то эта функция монотонна.
ДОКАЗАТЕЛЬСТВО.
Возьмем произвольные значения d и t, причем d £ t. В этом случае условию теоремы удовлетворяют следующие возможности:
у(d) = 0, у (t) = 0
у(d) = 0, у (t) = 1
у(d) = 1, у (t) = 1
Откуда следует, что для доказательства теоремы достаточно доказать следующее утверждение:
если d £ t, то у (d) = 1 у (t) = 1
Докажем это утверждение.
Если у(d) = 1, то всегда найдется интервал, для которого выполняется следующее условие:
xj1, xj2 … xjk|d = 1, где dj1 = dj2 = djk