Застосовування методів математичної статистики в технології машинобудування

Основні терміни і означення математичної статистики. Статистичний аналіз точності обробки за допомогою побудови кривих розподілу (методу великих вибірок). Закони розподілу випадкових величин. Статистичний аналіз точності обробки за допомогою методу точкових діаграм.

У машинобудуванні статистичні методи широко використовуються для оцінювання точності обробки деталей в ході діючого технологічного процесу їх виготовлення, настроювання металорізальних верстатів на розмір обробки, оцінювання стабільності технологічних процесів, прогнозування браку, контролю якості продукції і розв’язання інших технологічних задач переважно серійного і масового виробництва.

3.13.1. Основні терміни і означення математичної статистики,
які використовуються в технології машинобудування [12]

Математична статистика — наука про математичні методи систематизації і застосування статистичних даних для наукових і практичних висновків.

У математичній статистиці використовуються специфічні поняття, серед яких основними є:

- випробовування;

- подія;

- випадкова величина;

- розподіл випадкової величини;

- генеральна сукупність;

- вибірка;

- об’єм вибірки.

Випробуванням називають практичне виконання певного комплексу дій і умов (наприклад, однократне виконання деякого технологічного переходу механічної обробки).

Подією називають явище, що відбувається внаслідок випробування (наприклад, отримання певного дійсного значення технологічного розміру внаслідок однократного виконання технологічного переходу механічної обробки).

Події, що відбуваються під час багаторазового повторення випробовувань, називають масовими.

Якщо в результаті кожного випробування неодмінно відбувається певна подія А, то таку подію називають достовірною. Якщо в умовах даного випробування деяка подія В ніколи не може відбутись, то її називають неможливою. Якщо ж під час випробування подія С може відбутися, а може і не відбутися, то таку подію називають можливою або випадковою.

Якщо результатом масових випробувань є сукупність випадкових подій, які можна охарактеризувати кількісно, то цю кількісну характеристику (лінійний розмір, показник шорсткості, твердість матеріалу тощо) називають випадковою величиною. Наприклад, випадковою величиною може бути діаметр шийки валика як результат механічної обробки партії таких валиків на одному з технологічних переходів.

Розрізняють дискретні і безперервні випадкові величини.

Дискретна випадкова величина може приймати лише певні, найчастіше цілочислові значення. Наприклад, кількість бракованих деталей в партії може бути тільки цілим додатним числом.

Безперервна випадкова величини може приймати будь-які кількісні значення з безперервного ряду її можливих значень в межах певного інтервалу. Наприклад, розміри деталей, які утворюються в результаті механічної обробки, є безперервними випадковими величинами.

Під час випробувань деяка випадкова подія може відбуватися декілька разів. Нехай, наприклад, під час проведених N випробувань подія А відбулася f разів. Число f має назву частоти події. Відношення частоти події f до загальної кількості випробувань N називають частістю 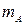події.

Таким чином,

. (50)

Якщо кількість випробувань досить велика, то частість подій приблизно дорівнює імовірності появи цих подій в майбутньому (зрозуміло, що за тих же умов).

Сукупність значень випадкової величини, отриманих під час масових випробувань, розташованих у висхідному порядку із зазначенням їх імовірності або частості, називають розподілом випадкової величини.

Однією з основних задач математичної статистики є розробка методів вивчення масових явищ або процесів на основі порівняно невеликої кількості випробувань. Ці методи мають своє наукове обґрунтування, яке називають теорією вибірок.

У відповідності з цією теорією групу предметів, об’єднаних деякою спільною ознакою або властивістю кількісного чи якісного характеру, називають статистичною сукупністю. Наприклад, партію деталей, оброблену зі сталими технологічними умовами на певній операції, можна розглядати як статистичну сукупність. Спільною ознакою може бути досліджуваний розмір поверхні або розмір між поверхнями.

Для обстеження великих сукупностей використовують вибірки з них. Таким чином, вибірка — це частина членів сукупності, відібраних із неї для отримання інформації про всю сукупність. У цьому випадку сукупність, що їх представляє вибірка, називають генеральною сукупністю.

Кількість членів вибірки складає її об’єм.

3.13.2. Статистичний аналіз точності механічної обробки
за допомогою побудови кривих розподілу (методу великих вибірок)

Статистичний аналіз проводять після того, як верстат пропрацює деякий час (1…2 години) для стабілізації температури системи ВПІД.

Для аналізу відбирається вибірка оброблених підряд одна за одною заготовок. Об’єм вибірки має складати 50…100 шт.

Для того, щоб за даними аналізу вибірки можна було робити висновки щодо певної ознаки генеральної сукупності, необхідно, щоб члени вибірки правильно її представляли, тобто вибірка має бути репрезентативною.

Під час статистичних досліджень технологічних переходів механічної обробки для забезпечення репрезентативності вибірки оброблених заготовок повинні виконуватись такі умови:

- всі заготовки мають оброблятися безперервно, на одному верстаті, одним інструментом, з однаковими режимами різання;

- верстат має працювати з приблизно однаковими зупинками для установлення й знімання заготовок, без тривалих перерв;

- всі заготовки мають бути виготовлені з одного й того ж матеріалу;

- під час обробляння заготовок вибірки різальний інструмент не повинен зніматися, переточуватися, правитися і піднастроюватися.

Після обробки всі заготовки вибірки вимірюються за допомогою універсального вимірювального інструмента з ціною поділки, яка не повинна перевищувати , де T – допуск вимірюваного розміру.

Розглянемо приклад. Припустимо, що на настроєному токарному напівавтоматі в партії заготовок розточується отвір в розмір Ø40Н9(^+0,062) мм.

Для аналізу відібрана вибірка послідовно оброблених деталей об’ємом 50 штук з такими розмірами (таблиця 7). Дійсні розміри отворів записані в таблицю у послідовності вимірювання деталей.

Таблиця 7

Дійсні розміри оброблених деталей

40,037	40,000	40,035	40,029	40,041
40,023	40,012	40,036	40,028	40,042
40,030	40,032	40,036	40,030	40,043
40,024	40,014	40,027	40,037	40,018
40,052	40,046	40,022	40,033	40,045
40,025	40,017	40,063	40,031	40,015
40,026	40,044	40,048	40,032	40,047
40,036	40,019	40,039	40,013	40,038
40,028	40,039	40,020	40,031	40,024
40,036	40,024	40,038	40,034	40,031

В результаті аналізу отриманої сукупності дійсних розмірів отворів будують криву розподілу у такій послідовності.

Спочатку визначають емпіричне поле розсіювання 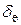досліджуваного розміру х, тобто інтервал, у якому знаходяться всі дійсні значення х. Цей інтервал знаходять як різницю найбільшого і найменшого значень х, тобто

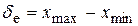. (51)

У випадку, що розглядається, 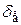= 40,063 – 40,000 = 0,063 мм.

Далі поле розсіювання розбивають на певну кількість інтервалів k (найчастіше k = 8...11) і визначають ширину інтервалу 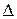за формулою

. (52)

Прийнявши k = 7, отримаємо 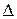= 0,063/7 = 0,009 мм.

Результат обчислення 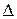допускається дещо округляти в більшу сторону. Подальші результати аналізу сукупності дійсних розмірів можна оформити у вигляді таблиці 8.

Таблиця 8

Результати підрахунку частот інтервалів

№ інтер-валу	Границі інтервалу, мм	Підрахунок частот	Частота, f	Частість, m	Емпірична щільність розподілу, y е
	Від 40,000 до 40,009	//		0,04	4,4
	Поверх 40,009 до 40,018	/////		0,10	11,1
	Поверх 40,018 до 40,027	///// ///		0,18	20,0
	Поверх 40,027 до 40,036	///// ///// ///// ////		0,38	42,2
	Поверх 40,036 до 40,045	///// /////		0,20	22,0
	Поверх 40,045 до 40,054	////		0,08	8,9
	Поверх 40,054 до 40,063	/		0,02	2,2

Емпіричний розподіл випадкової величини можна показати графічно (рис. 37) у вигляді полігона розподілу або гістограми розподілу).

Очевидно, що значення частостей m_i будуть залежати від ширини вибраного інтервалу. Щоб позбутися цього, розглядають емпіричну щільність розподілу випадкової величини, розуміючи під останньою відношення частості до величини інтервалу

, (53)

де і – порядковий номер інтервалу.

У цьому випадку вид графіка не залежить від величини інтервалу ∆. Цей інтервал навіть можна вибирати різним на різних ділянках графіка. Зі збільшенням кількості деталей в партії, підвищенням точності їх вимірювання і наближенням ∆ до нуля графік емпіричної щільності розподілу наближається до гладкої кривої, яку називають емпіричною диференціальною кривою розподілу або розподілом випадкової величини.

Для того, щоб за знайденим розподілом розмірів вибірки спрогнозувати результати обробки заготовок, які складають генеральну сукупність, потрібно знайдений (емпіричний) закон розподілу замінити теоретичним законом, який за формою був би близьким до емпіричного.

Рис. 37. Графіки емпіричної і теоретичної характеристик розподілу безперервної випадкової величини (розміру x)

В залежності від технологічних умов, розміри оброблених заготовок можуть підпорядковуватися різним законам розподілу. В технології машинобудування практичне застосування мають такі закони:

- нормального розподілу (закон Гауса);

- рівнобедреного трикутника (закон Сімпсона);

- закон рівної імовірності;

- ексцентриситету (закон Релея).

Детальніше розглянемо особливості застосування і основні характеристики цих законів.

Закон нормального розподілу (закон Гаусса)

Дослідженнями вчених (професори А.Б. Яхін, А.А. Зиков та ін.) встановлено, що емпіричний розподіл розмірів заготовок, оброблених на настроєному верстаті, найчастіше є близьким до закону нормального розподілу. Рівняння диференціальної кривої нормального розподілу має такий вид

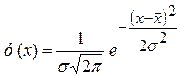, (54)

де у – теоретична щільність розподілу; 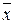- середнє значення розміру х;
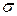– середнє квадратичне відхилення випадкової величини (розміру х);
= 2,718 – основа натуральних логарифмів.

Значення 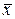та σ можна знайти за формулами

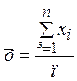; (55)

або

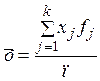; (56)

, (57)

або

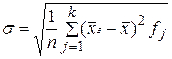, (58)

де n – кількість заготовок у вибірці (об’єм вибірки); x_i – значення дійсного розміру і -ї обробленої заготовки; 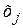– середній розмір заготовок j- го інтервалу; 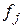– частота j- го інтервалу.

Крива, що характеризує закон нормального розподілу, показана на рис. 38.

Аналіз рівняння (54) показує, що крива нормального розподілу симетрична відносно ординати точки 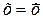. У цій точці крива має максимум

.

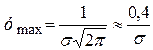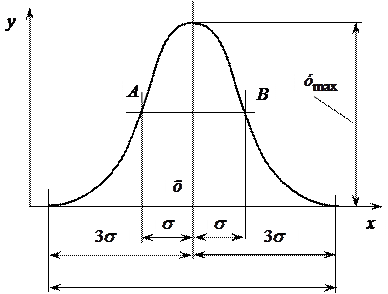
Рис. 38. Крива нормального розподілу (закон Гаусса)

На відстані 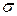від вершини крива моє дві точки перегину (точки А і В). ордината точок перегину складає

.

Вітки кривої асимптотично наближаються до осі абсцис. В практичних розрахунках зазвичай вважають, що на відстані від вершини кривої її вітки дотикаються до осі абсцис.

Зі збільшенням 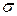значення ординати зменшується, а теоретичне поле розсіювання 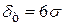збільшується. Це свідчить про більше розсіювання розмірів і, відповідно, про меншу точність. Таким чином, величина 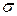є мірою розсіювання або мірою точності. Вплив величини 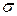на форму кривої нормального розподілу показано на рис. 39.

	y

Рис. 39. Вплив середнього квадратичного відхилення на форму кривої Гаусса

Закону нормального розподілу найчастіше підпорядковуються розміри заготовок, оброблених на настроєних верстатах з точністю 8, 9, 10 і грубіших квалітетів точності.

Закон рівнобедреного трикутника (закон Сімпсона)

Розподіл розмірів заготовок, оброблених з точністю 7 і 6 квалітетів, найчастіше підпорядковуються закону Сімпсона, який має вигляд рівнобедреного трикутника (рис. 40).

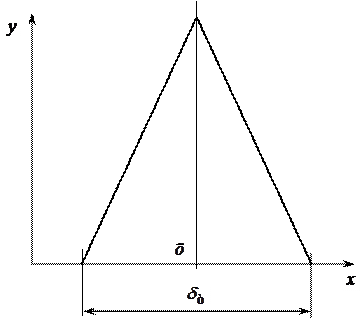Рис. 40. Розподіл розмірів оброблених заготовок за законом Сімпсона

Теоретичне поле розсіювання у цьому випадку складає

.

Величина середнього квадратичного відхилення 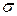визначається за формулами (57) або (58).

Закон рівної імовірності

Розподіл розмірів заготовок в інтервалі від a до b (рис. 41) за законом рівної імовірності відображається прямокутником з основою 2 l.

Закону рівної імовірності підпорядковуються розміри заготовок підвищеної точності (5, 6 квалітети) за умови обробки цих заготовок з використанням способу спробних робочих ходів і промірів. Через складність отримання розмірів дуже високої точності імовірність попадання розміру заготовки у середину поля допуску чи його краї стає однаковою.

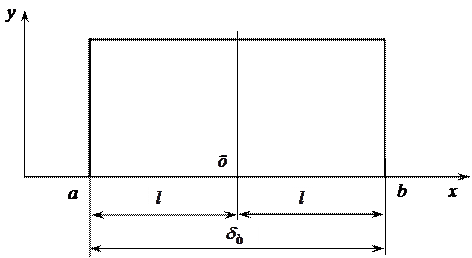
Рис. 41. Розподіл розмірів оброблених заготовок за законом
рівної імовірності

Величина середнього квадратичного відхилення 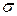визначається за формулою

.

Закон ексцентриситету (закон Релея)

Розподіл таких величин, як неспіввісність, биття, непаралельність, неперпендикулярність, некруглість, нециліндричність, непрямолінійність, які характеризуються їх абсолютними значеннями (тобто без урахування знаку) підпорядковуються закону ексцентриситету (закон Релея). Диференціальна функція розподілу цього закону визначаєтьсяя залежністюмає вигляд

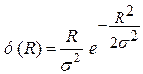, (59)

де 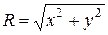– змінна величина ексцентриситету або биття; х і у координати зміщеної осі (рис. 42); 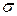– середнє квадратичне відхилення координат х і у за умови, що .

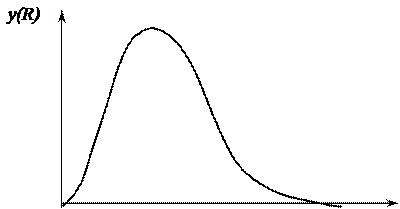
Графік функції (59) показаний на рис. 43.

Особливістю закону Релея є те, що в його основі лежить нормальний розподіл, оскільки координати х і у точки кінця радіуса-вектора R розподілені нормально, але розподіл R не підпорядковується закону Гауса. Зв'язок між , 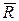та 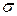відображають такі залежності

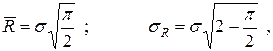
де 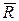– середнє арифметичне значення випадкової величини R; – середнє квадратичне відхилення R від .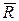

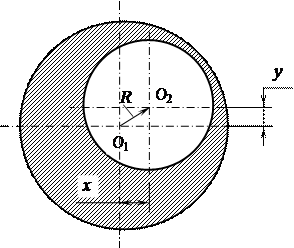Рис. 42. Ексцентриситет осі (О ₂) отвору відносно осі (О ₁)
зовнішньої циліндричної поверхні

		R

Рис. 43. Графік функції розподілу розмірів за законом Релея

Продовжимо розгляд прикладу (див. с. 105). З візуального аналізу отриманих гістограми і полігону розподілу (див. рис. 37) можна зробити висновок, що з описаних вище законів розподілу найближчим є закон Гаусса.

Для побудови теоретичної кривої розподілу потрібно зайти величини 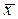і 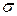. Це можна зробити за формулами (56) і (58). Для прикладу, що розглядається, 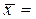40,031 мм, 0,011 мм.

Замінивши емпіричний розподіл, потрібно оцінити справедливість цієї заміни. Це можна зробити з використанням критерію згоди Колмогорова. Методика використання цього критерію описана в [14].

Подальший аналіз результатів вимірювань здійснюється за допомогою таблиць унормованих законів розподілу. Для можливості використання таких таблиць розмірну незалежну змінну х замінюють безрозмірною незалежною змінною t, яка зв’язана з х таким співвідношенням

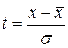. (60)

З урахуванням (60) рівняння (54) можна записати у вигляді

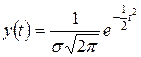. (61)

Важливою особливістю виразу (61) є те, що в інтервалі ±3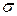із серединою в точці, що відповідає значенню 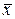, знаходиться 99,7% усієї площі під кривою розподілу, тобто теоретичне поле розсіювання складає приблизно 6 σ. Крім того, крива Гаусса є симетричною відносно середнього розміру 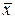і тому

.

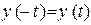Далі, показавши на осі х (див. рис. 37) поле допуску досліджуваного технологічного розміру, можна визначити відсоток імовірного браку (виправного та невиправного).

Відсоток виправного браку для отвору (для вала – невиправного) складе

, (62)

де 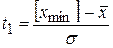– координата по осі t нижньої границі поля допуску
(див. рис. 37), – найменше допустиме значення технологічного розміру.

Відповідно відсоток невиправного браку для отвору (для вала –виправного)

, (63)

де 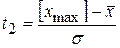– координата по осі t нижньої границі поля допуску, 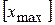– найбільше допустиме значення технологічного розміру.

Величини Ф(t ₁) та Ф(t ₂) визначаються за таблицею функції Лапласа, яка є в додатку Б [14].

Аналіз точності технологічного переходу можна виконати також за допомогою коефіцієнта точності виконання K _т і коефіцієнта зміщення настроєння Е.

Коефіцієнт точності виконання

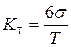, (64)

де 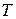– допуск досліджуваного технологічного розміру.

Коефіцієнт зміщення настроєння

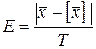, (65)

де – середнє значення заданого технологічного розміру.

Визначений за формулою (65) фактичний коефіцієнт зміщення настроєння порівнюється з допустимим

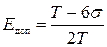. (66)

Слід зазначити, що зміщення середини кривої розподілу відносно середини поля допуску може передбачатись для компенсації систематичних похибок, що закономірно змінюються (наприклад, похибки, що спричиняється розмірним зносом різального інструмента), тільки за умови, якщо 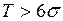. Якщо ж 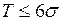, то таке зміщення призводить до збільшення браку і тому недоцільне.

Таким чином, робота без браку забезпечується, якщо виконуються умови

К _т ≤ 1; (67)

Е ≤ Е _доп. (68)

3.13.3. Статистичний аналіз точності механічної обробки за
допомогою методу точкових діаграм

Для настроювання верстата під час його підготовки до механічної обробки партії заготовок потрібно знати основні статистичні характеристики розподілу розміру 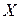, який отримується на цьому переході технологічної операції, як безперервної випадкової величини.

До таких характеристик відносять: відсутність чи наявність стійкості технологічного процесу, відсутність чи наявність впливу факторів, що спричиняють систематичні похибки, значення середньоквадратичного відхилення контрольованого розміру, закон його розподілу тощо. Більшість з цих характеристик можна визначити за допомогою методу точкових діаграм.

Статистичний аналіз методом точкових діаграм виконують таким чином.

Вибірки об’ємом n = 5...10 штук беруться безперервно або через певні фіксовані проміжки часу роботи верстата (наприклад через 15...20 хвилин). Верстат має працювати з приблизно однаковими зупинками для встановлення й знімання заготовок, без тривалих перерв і без піднастроювання. У кожної з відібраних заготовок визначають дійсний розмір 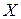. 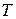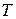Ці розміри визначаються за допомогою універсального вимірювального інструмента, у якого ціна поділки шкали має становити (1/6...1/10), де – допуск контрольованого розміру.

Для кожної вибірки визначають середній розмір

(69)

і середньоквадратичне відхилення

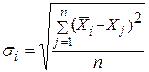, (70)

де – кількість деталей у вибірці, 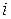– номер вибірки, 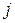– номер деталі у вибірці.

За результатами вимірювань і розрахунків будують точкові діаграми. Ці діаграми, в залежності від технологічних особливостей операції і стану обладнання, можуть мати різний вигляд. Наприклад, у випадку, якщо різання здійснюється інструментом, доведеним алмазним кругом, і з ефективним охолодженням (тобто, коли початковий знос і видовження інструмента від нагрівання незначні), точкова діаграма матиме вигляд, показаний на рис. 44.

У даному випадку змінення середнього розміру 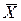з переходом від попередньої вибірки до наступної пояснюється впливом на точність механічної обробки факторів, що спричиняють появу систематичних похибок, які закономірно змінюються. Такими факторами можуть бути, наприклад, розмірний знос різального інструмента або температурні деформації елементів системи ВПІД.

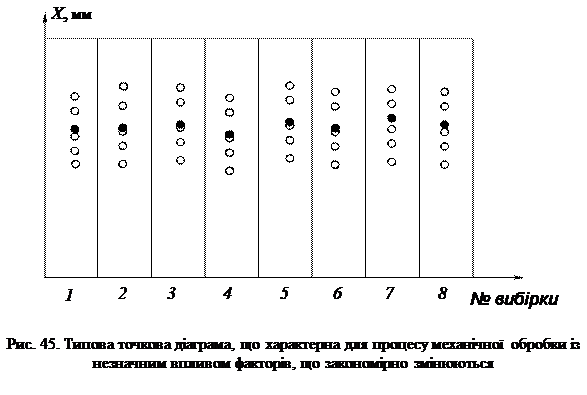
Якщо ж вплив таких факторів незначний, то точкова діаграма матиме вигляд, показаний на рис. 45.

Для оцінювання технологічної стійкості переходу будують точкову діаграму середньоквадратичних відхилень 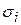вибірок. Типова точкова діаграма стійкого переходу показана на рис. 46. Якщо значення 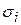для різних вибірок суттєво відрізняються, то перехід вважається технологічно нестійким. Приклад точкової діаграми такого переходу показаний на рис. 47.

Втрату стійкості можуть спричинити, наприклад, надто великі люфти між рухомими деталями елементів системи ВПІД, значний розкид фізико-механічних властивостей матеріалу заготовок тощо. У цьому випадку слід виявити причини нестійкості, усунути їх і лише після цього настроїти верстат і обробляти заготовки.

ЛІТЕРАТУРА

1. Балакшин Б.С. Основы технологии машиностроения. Учебник для машиностроительных специальностей вузов. /Б.C. Балакшин. ― М.: Машиностроение, 1969. ― 558 с.

2. Дерібо О.В. Теоретичні основи технології виробництва деталей та складання машин. Частина 1: практикум /О.В. Дерібо О.В. Ж. П. Дусанюк, С.В. Репінський ― Вінниця: ВНТУ, 2010. ― 114 с.

3. Дерібо О.В. Методичні вказівки до виконання курсового проекту з дисципліни «Технологія обробки типових деталей та складання машин» / О.В. Дерібо, Ж.П. Дусанюк, В.П. Пурдик ― Вінниця, 2009. ― 102 с. Електронний ресурс: http://www.vstu.vinnica.ua/ua/inst/inmt/site_tam/.

4. Допуски и посадки. Справочник. В 2-х ч. Ч. 1 [В.Д. Мягков,
М.А. Палей, А.Б. Романов и др.]; под ред. В.Д. Мягкова ― Л.: Машиностроение. Ленингр. отд-ние, 1983. ― 543 с.

5. Допуски и посадки. Справочник. В 2-х ч. Ч. 2 [В.Д. Мягков,
М.А. Палей, А.Б. Романов и др.]; ― Л.: Машиностроение. Ленингр.
отд-ние, 1983. ― 448 с.

6. Кован В.М. Основы технологии машиностроения [В.М. Кован, В.С. Корсаков, А.Г. Косилова и др.] Под ред. В.С. Корсакова.
― М.: Машиностроение, 1977. ― 416 с.

7. Колесов И.М. Основы технологии машиностроения. Учебник для машиностроительных специальностей вузов. /И.М. Колесов. ― М.: Высшая школа, 2001. ― 591 с.

8. Маталин А.А. Технология машиностроения: Учебник для машиностроительных специальностей вузов. /А.А. Маталин. ― Л.: Машиностроение, 1985. ― 496 с.

9. Корсаков В.С. Основы конструирования приспособлений в машиностроении. В.С. Корсаков. — М.: Машиностроение, 1977. — 288 с.

10. Расчеты экономической эффективности новой техники Справочник. [К.М. Великанов, В.Ф. Власов, Г.А. Краюхин и др. ] Под общ. ред.
К. М. Великанова. — Л.: Машиностроение. 1990. — 488 с.

11. Сборник задач и упражнений по технологии машиностроения. Под ред. О.А. Горленко. ― М.: Машиностроение, 1988. ― 216 с.

12. Солонин И.С. Математическая статистика в технологии машиностроения. / И.С. Солонин. ― М.: Машиностроение, 1972. ― 216 с.

13. Справочник технолога-машиностроителя: в 2 т. Т. 1 /
[В.Б. Борисов, Е.И. Борисов, В.Н. Васильєв и др.]; под ред. А. Г. Косиловой и Р.К. Мещерякова. — М.: Машиностроение, 1985. — 656 с.

14. Теоретичні основи технології виробництва деталей та складання машин. Лабораторний практикум. [О.В. Дерібо, Ж.П. Дусанюк, О.М. Мироненко та ін.] ― Вінниця: ВНТУ, 2006. ― 119 с.

15. Технология машиностроения. В 2 кн. Кн.1. Основы технологии машиностроения: Учеб. пособие для вузов [Э.Л. Жуков, И.И. Козарь,
С.Л. Мурашкин и др.]; Под ред. С.Л. Мурашкина. ― М.: Высш. шк. 2003.
― 278 с.

16. А.В. Якимов. Технология машиностроения: Учебник для машиностроительных специальностей вузов. / А.В. Якимов, В.Н Царюк, А.А. Якимов и др. ― Одесса.: Астропринт, 2001. — 608 с.

17. Базирование и базы в машиностроении. Термины и определения: ГОСТ 21495-76. — [Чинний від 1977-01-01] М.: Изд-во стандартов, 1987. — 35 с.

18. Опоры, зажимы и установочные устройства. Графические обозначения: ГОСТ 3.1107-81 — [Чинний від 1982-07-01] ― М.: Изд-во стандартов, 2003. — 10 с.

19. Единая система технологической документации. Термины и определения основных понятий: ГОСТ 3.1109-82 — [Чинний від 1983-01-01] ― М.: Изд-во стандартов, 2003. — 14 с.

20. Технологическая подготовка производства. Термины и определения основных понятий: ГОСТ 14.004-83 — [Чинний від 1983-07-01] ― М.: Стандартинформ, 2005. — 8 с.

21. Единая система технологической документации. Общие требования к комплектности и оформлению документов на типовые и групповые технологические процессы (операции): ГОСТ 3.1121-84 — [Чинний від 1986-01-01] ― М.: Стандартинформ, 2006. — 46 с.

Дата добавления: 2014-01-07