
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Характеристики непрерывных источников
|
|
|
|
Любой источник информации создает случайный выход: если выход известен точно, его не надо передавать. Источник дискретной информации с алфавитом из символов выдает последовательность символов из алфавита. Так, компьютеры и устройства хранения информации, такие как магнитные или оптические диски, имеют дискретный выход. Пусть для каждого символа алфавита задана вероятность выбора, где. Возьмем две математические модели дискретных источников. Символы выходной последовательности дискретного источника без памяти (ДИБП) статистически независимы друг от друга. Если выходные символы дискретного источника статистически взаимосвязаны, как, например, в тексте на русском или другом языке, можно построить стационарную модель. Совместные вероятности двух последовательностей дискретного стационарного источника: и, длины одинаковы при и любых сдвигах.
Характеристики дискретных источников
Количество информации в событии  относительно события
относительно события  равно
равно
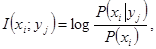 (2.1)
(2.1)
где 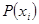 - собственная (априорная) вероятность
- собственная (априорная) вероятность 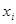 ,
, 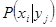 - вероятность
- вероятность 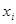 при условии, что
при условии, что 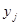 известно. Если
известно. Если  и
и 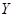 статистически независимы,
статистически независимы, 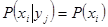 и
и 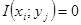 . То есть, независимые события информации друг о друге не несут. Используя (2.1), можно показать, что количество информации, доставляемое
. То есть, независимые события информации друг о друге не несут. Используя (2.1), можно показать, что количество информации, доставляемое  относительно
относительно  , равно таковому, доставляемому
, равно таковому, доставляемому  относительно
относительно  , то есть
, то есть 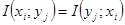 . Взаимная информация
. Взаимная информация 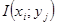 между парой событий может быть
между парой событий может быть 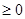 и
и 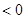 .
.
Согласно (2.1), собственная информация  события
события  :
:
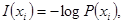 (2.2)
(2.2)
дает количество информации в  или в любом другом
или в любом другом  , однозначно с ним связанным (
, однозначно с ним связанным (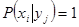 ). Единица измерения информации зависит от выбора основания
). Единица измерения информации зависит от выбора основания 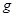 логарифма. При
логарифма. При  (
(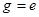 ) эта единица – бит (нат - натуральная единица). Чем вероятнее событие, тем меньше информации в нем. Если возможно лишь
) эта единица – бит (нат - натуральная единица). Чем вероятнее событие, тем меньше информации в нем. Если возможно лишь 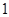 событие
событие 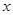 (
(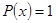 ), то
), то 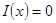 .
.
Пример 2.1.1. Пусть дискретный источник равновероятно выдает двоичную цифру  или
или 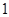 каждые
каждые 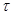 секунд. Количество информации, доставляемое цифрой,
секунд. Количество информации, доставляемое цифрой, 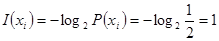 (бит),
(бит),  Пусть последовательные цифры на выходе источника статистически независимы, то есть источник не имеет памяти. Всего есть
Пусть последовательные цифры на выходе источника статистически независимы, то есть источник не имеет памяти. Всего есть  возможных
возможных 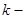 битовых блоков источника, каждый – с вероятностью
битовых блоков источника, каждый – с вероятностью 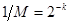 и длительностью
и длительностью 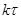 . Собственная информация блока за время
. Собственная информация блока за время 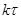 равна
равна 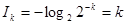 (бит).
(бит).
Определим условную собственную информацию
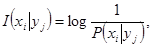 (2.3)
(2.3)
где 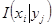 - собственная информация события
- собственная информация события  при известном
при известном  .
.
Комбинируя (2.1), (2.2) и (2.3), получим
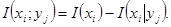 (2.4)
(2.4)
Средняя взаимная информация случайных величин  и
и 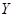 в расчете на символ
в расчете на символ
 (2.5)
(2.5)
где 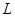 и
и 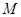 - объемы алфавитов
- объемы алфавитов  и
и 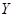 , соответственно. Можно показать, что
, соответственно. Можно показать, что 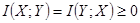 , и
, и 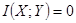 для статистически независимых
для статистически независимых  и
и 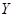 .
.
Средняя условная собственная информация - условная энтропия,
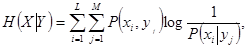 (2.6)
(2.6)
где 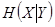 - неопределенность в значениях
- неопределенность в значениях  (дополнительная информация, содержащаяся в
(дополнительная информация, содержащаяся в  ) после наблюдения
) после наблюдения 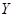 .
.
Энтропия источника равна его средней собственной информации на символ,
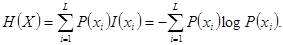 (2.7)
(2.7)
Из (2.1), (2.5), (2.6) и (2.7) следует
 (2.8)
(2.8)
Из (2.8) и 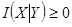 следует
следует  и
и 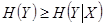 , где равенство верно, если
, где равенство верно, если  статистически не зависит от
статистически не зависит от 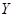 . Величина
. Величина  равна уменьшению среднего значения неопределенности значений
равна уменьшению среднего значения неопределенности значений  (
(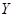 ) за счет измерения
) за счет измерения 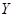 (
( ). Пусть
). Пусть  - длительность символа источника. Производительность источника - среднее количество информации, выдаваемое им в единицу времени,
- длительность символа источника. Производительность источника - среднее количество информации, выдаваемое им в единицу времени,
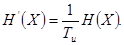 (2.9)
(2.9)
Пример 2.1.2. Возьмем источник, выдающий последовательность независимых символов:  - с вероятностью
- с вероятностью 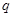 , и
, и 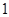 - с вероятностью
- с вероятностью 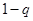 . Энтропия двоичного источника
. Энтропия двоичного источника 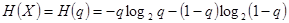 . Максимальное значение
. Максимальное значение  бит (при равновероятных символах), а минимальное -
бит (при равновероятных символах), а минимальное - 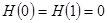 (если возможна передача лишь одного символа).
(если возможна передача лишь одного символа).
Для источника с объемом алфавита 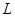 выразим
выразим
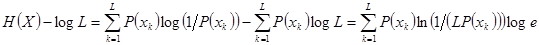 .
.
Так как  (
(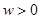 ), то
), то 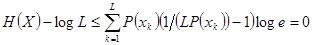 , или
, или
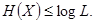 (2.10)
(2.10)
Наибольшее значение: 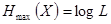 (информационная емкость алфавита источника), достигается, если символы равновероятны:
(информационная емкость алфавита источника), достигается, если символы равновероятны:  ,
, 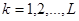 . Для передачи количества информации
. Для передачи количества информации  от источника с энтропией
от источника с энтропией  требуется
требуется 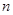 символов, а от источника с энтропией
символов, а от источника с энтропией 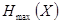 - минимальное их число
- минимальное их число
 (2.11)
(2.11)
где 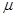 - допустимая степень сжатия сообщений,
- допустимая степень сжатия сообщений, 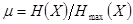 . Величина
. Величина  называется избыточностью источника.
называется избыточностью источника.
Пусть есть блок из 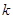 случайных величин
случайных величин 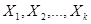 с совместной вероятностью
с совместной вероятностью 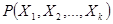 . Пусть
. Пусть 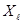 ,
, 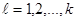 , имеет алфавит
, имеет алфавит 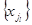 ,
, 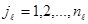 , с объемом
, с объемом 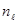 . Энтропия этого блока, согласно (2.7),
. Энтропия этого блока, согласно (2.7),
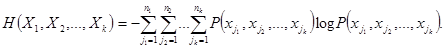 (2.12)
(2.12)
Так как 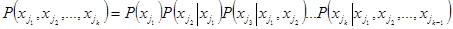 , из (2.12) следует
, из (2.12) следует
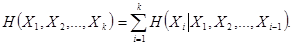 (2.13)
(2.13)
Так как  , где
, где 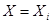 и
и  , из (2.13) имеем:
, из (2.13) имеем:
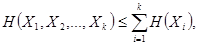 (2.14)
(2.14)
где равенство верно, если 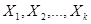 не зависят друг от друга.
не зависят друг от друга.
Аналоговый источник выдает непрерывный сигнал 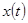 - реализацию случайного непрерывного процесса
- реализацию случайного непрерывного процесса 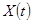 . Так, в радиовещании источник выдает звуковой сигнал (речь или музыку), а в телевизионном вещании, кроме звука, - и подвижное изображение. Стационарный процесс
. Так, в радиовещании источник выдает звуковой сигнал (речь или музыку), а в телевизионном вещании, кроме звука, - и подвижное изображение. Стационарный процесс 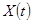 с ограниченной полосой спектра по частоте представим рядом Котельникова
с ограниченной полосой спектра по частоте представим рядом Котельникова 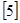 :
:
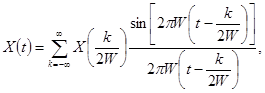 (2.15)
(2.15)
где 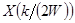 - непрерывные отсчеты
- непрерывные отсчеты 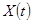 , взятые со скоростью Найквиста
, взятые со скоростью Найквиста  1/с,
1/с, 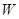 - верхняя граница спектра процесса
- верхняя граница спектра процесса 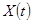 . Разложение (2.15) заменяет аналоговый источник эквивалентным с дискретным временем. Квантование отсчетов рядом дискретных значений вносит случайные искажения в точность представления отсчетов - шум квантования
. Разложение (2.15) заменяет аналоговый источник эквивалентным с дискретным временем. Квантование отсчетов рядом дискретных значений вносит случайные искажения в точность представления отсчетов - шум квантования 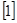 .
.
Пусть  и
и 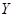 - случайные непрерывные величины с совместной плотностью вероятности
- случайные непрерывные величины с совместной плотностью вероятности 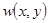 и собственными плотностями вероятности
и собственными плотностями вероятности 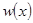 и
и 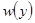 . Средняя взаимная информация величин
. Средняя взаимная информация величин  и
и 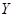 :
:
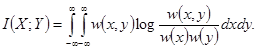 (2.16)
(2.16)
Сообщение  (
(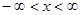 ) непрерывного источника квантуем с шагом
) непрерывного источника квантуем с шагом 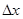 . Получим дискретную величину
. Получим дискретную величину 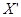 - множество возможных значений
- множество возможных значений 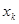 отсчетов
отсчетов  , с энтропией (см. (2.7))
, с энтропией (см. (2.7)) 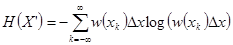 . Далее,
. Далее, 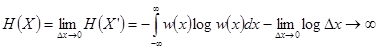 , где
, где  - энтропия непрерывного источника. В отличие от
- энтропия непрерывного источника. В отличие от  дифференциальная энтропия
дифференциальная энтропия 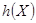 конечна по величине, но не имеет смысла собственной информации,
конечна по величине, но не имеет смысла собственной информации,
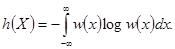 (2.17)
(2.17)
Пример 2.2.1. Из(2.17)выразим дифференциальную энтропию гауссовской величины  с распределением
с распределением 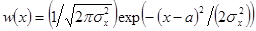 , средним
, средним  и дисперсией
и дисперсией 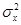 :
:
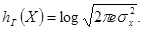 (2.18)
(2.18)
При заданной дисперсии среди случайных непрерывных величин с разными законами распределения наибольшую дифференциальную энтропию имеет гауссовская величина 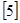 .
.
Условная дифференциальная энтропия случайной непрерывной величины  при заданной
при заданной 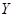 :
:
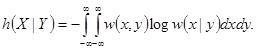 (2.19)
(2.19)
Учитывая (2.16), (2.17) и (2.19), 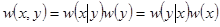
 , найдем
, найдем
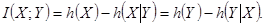 (2.20)
(2.20)
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 292; Нарушение авторских прав?; Мы поможем в написании вашей работы!