Свойства непрерывных функций

Теорема 1. Если функци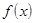и и 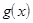непрерывны в точке 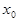, то в этой точке непрерывны следующие функции:

1) с, с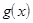, с = const; 3) ×;

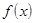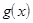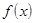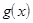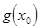2) ± ; 4) , ¹ 0.

Доказательство. Докажем третье утверждение теоремы. Поскольку предел произведения равен произведению пределов, то

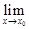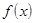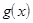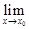
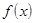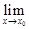
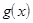(×) = × = ×. (1)

Равенство (1) и означает непрерывность функции 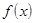×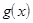. Остальные утверждения доказываются аналогично.

Рассмотрим две функци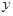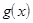и = и 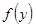. Сложная функция 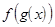называется суперпозицией данных функций. Например, 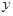= – суперпозиция трех функций: логарифмической, тригонометрической и степенной.

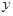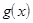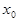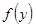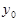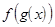Теорема 2. Если функция = непрерывна в точке , а функция непрерывна в точке = ,то сложная функция непрерывна в точке .

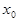Доказательство. Поскольку функция 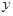= 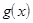непрерывна, то

= = .

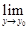
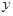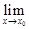
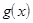Используя первое следствие §7, получим

= () = () = ().

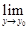
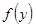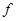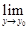
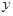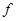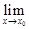
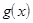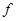Последнее равенство можно переписать так:

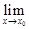
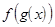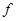= (). (2)

Равенство (2) и означает непрерывность сложной функции в точке .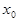

Замечание. Теорема 2 даёт правило замены переменных при вычислении пределов непрерывных функций

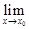
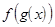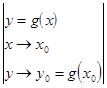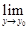
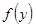= = . (3)

Теорема 3. Если функция 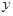= 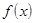непрерывна в точке 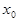и 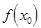¹ 0, то существует окрестность 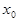, в которой функция 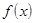сохраняет свой знак (без доказательства).

Функцию называют элементарной, если она получается путём конечного числа арифметических операций и суперпозиций пяти основных элементарных функций. Например, 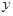= 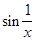, 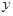= 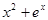– элементарные функции, а функции 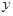= sgn x, 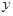= 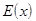, 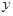= 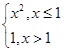не являются элементарными. Функция Дирихле также неэлементарная.

Поскольку все пять основных элементарных функций являются непрерывными в своих областях определения, то из теорем 1,2 вытекает следующее следствие: всякая элементарная функция непрерывна в своей области определения. Заметим, что для неэлементарных функций это утверждение не справедливо.

Теорема 4. Всякая непрерывная на отрезке [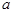,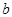] функция 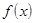ограничена этом отрезке, достигает на нём своих наибольшего и наименьшего значений M = sup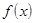, m = inf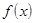и принимает на нём все промежуточные значения из отрезка [ m, M]. (Без доказательства).

Замечание. Для функции, непрерывной на интервале (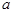,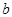), теорема 4 не справедлива. Например, функция 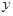= 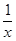непрерывна на интервале (0,1), но не ограничена на нём и не достигает своих наибольшего и наименьшего значений.

Следствие. Если непрерывная на отрезке [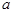,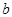] функция 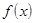принимает на его концах значения разных знаков, то найдётся хотя бы одна точка 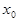Î(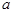,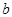), в которой функция обращается в нуль, т.е. 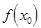= 0. Доказательство очевидно.

Следствие теоремы 4 часто используется для приближенного нахождения корней уравнения.

Пример. Найти корень уравнения 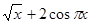= 0.

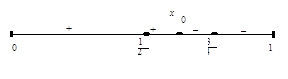
Решение. Рассмотрим функцию 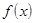=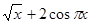. Она элементарная, поэтому непрерывная для всех 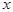³ 0.

Вычислим 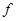(0) = 2 и 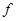(1) = –1.

Т.к. значения функции разных знаков, то корень уравнения 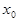лежит в интервале (0,1), т.е. 0 <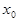< 1. Разделим отрезок [0,1] пополам и вычислим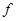 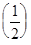= 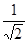. Отсюда следует, что 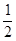< < 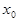1. Разделим отрезок [1/2,1] пополам и вычислим =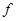

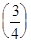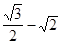=< 0. Отсюда следует, что 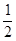< < 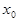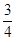, т.е. мы уже вычислили корень уравнения с точностью до 0,25. Продолжая этот процесс, можно вычислить корень с любой наперед заданной точностью.

Дата добавления: 2014-01-07