
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тригонометрический ряд Фурье
|
|
|
|
Ряд Фурье по ортонормированной системе тригонометрических функций (3) §1 называется тригонометрическим рядом Фурье. В дальнейшем будем называть его просто рядом Фурье.
Чаще в тригонометрический ряд Фурье разлагают функцию не по ортонормированной системе, а по ортогональной ненормированной системе
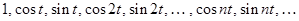
 (1)
(1)
Ряд Фурье записывается в виде
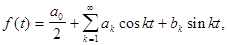 (2)
(2)
при этом коэффициенты, согласно (12) §2 определяются формулами
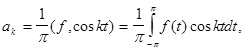
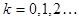 (3)
(3)

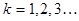 (4)
(4)
Разложение (2) справедливо только на отрезке 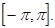 Но поскольку правая часть (2) - функция периодическая, то продолжая функцию
Но поскольку правая часть (2) - функция периодическая, то продолжая функцию  заданную на отрезке
заданную на отрезке  периодически с периодом
периодически с периодом 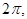 добьемся того, что разложение (2) будет справедливо на всей числовой оси.
добьемся того, что разложение (2) будет справедливо на всей числовой оси.
Пусть теперь функция  задана на отрезке
задана на отрезке 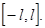 Введем замену
Введем замену 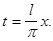 Тогда
Тогда 
 Запишем ряд Фурье для функции
Запишем ряд Фурье для функции 
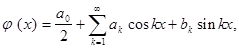

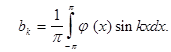
Вернемся теперь к старой переменной 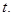 Тогда
Тогда 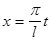 и
и
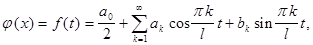 (5)
(5)


 (6)
(6)
Аналогично найдем
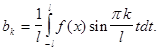 (7)
(7)
Если функцию  считать периодической с периодом
считать периодической с периодом 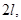 то разложение (5) будет справедливо на всей числовой оси.
то разложение (5) будет справедливо на всей числовой оси.
Пусть функция  задана на отрезке
задана на отрезке  Продолжим ее периодически на всю числовую ось с периодом
Продолжим ее периодически на всю числовую ось с периодом 
тогда 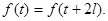
Докажем, что для периодической функции с периодом 
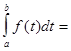
 (8)
(8)
Действительно,
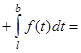
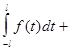

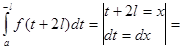


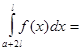

Равенство (8) доказано. Учитывая, что 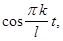
 также периодические функции с периодом
также периодические функции с периодом  найдем, что
найдем, что

 (9)
(9)
Аналогично,
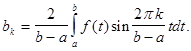 (10)
(10)
 (11)
(11)
Легко убедиться, что

Отсюда следует, что четная функция разлагается в ряд Фурье только по косинусам, а нечетная - только по синусам.
Пример. Разложить функцию 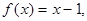
 в ряд Фурье.
в ряд Фурье.

Решение. 1-й способ. Продолжим функцию 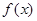 периодически с периодом
периодически с периодом 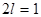 (см. рис. 4), получим функцию
(см. рис. 4), получим функцию
 (12)
(12)



2-й способ. Доопределим функцию 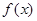 на отрезке
на отрезке 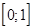 нулем, продолжим эту новую функцию
нулем, продолжим эту новую функцию 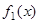 четным образом на отрезок
четным образом на отрезок  а затем периодически с периодом
а затем периодически с периодом  Получим функцию
Получим функцию 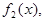 четную.
четную.
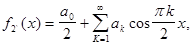 (13)
(13)


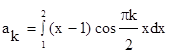
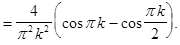
3-й способ. Доопределим функцию 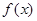 на отрезке
на отрезке 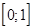 нулем, продолжим эту новую функцию
нулем, продолжим эту новую функцию 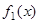 нечетным образом на отрезок
нечетным образом на отрезок  а затем периодически с периодом
а затем периодически с периодом  Получим нечетную функцию
Получим нечетную функцию  (14)
(14)

Заметим, что на отрезке  ряды (12,13,14) сходятся в среднем квадратичном к функции
ряды (12,13,14) сходятся в среднем квадратичном к функции 
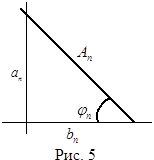
Преобразуем n- ое слагаемое ряда (5) (см. рис. 5)

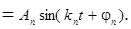 (15)
(15)
Выражение (15) называется n- ой гармоникой,  амплитудой,
амплитудой,  частотой,
частотой,  начальной фазой.
начальной фазой.
С учетом (15) ряд (5) можно записать так:
 (16)
(16)
Совокупность амплитуд 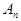 и частот
и частот  называют дискретным спектром функции
называют дискретным спектром функции 
Учитывая, что
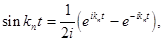

n-ю гармонику можно записать в виде:
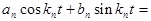
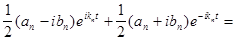
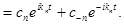 (17)
(17)
Полагая  и учитывая (17), ряд Фурье (5) можно записать в комплексном виде
и учитывая (17), ряд Фурье (5) можно записать в комплексном виде 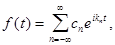
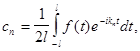
 (18)
(18)
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 444; Нарушение авторских прав?; Мы поможем в написании вашей работы!