
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доказательство. Т.к. а интеграл сходится, то согласно признаку Вейерштрасса (см
|
|
|
|
Т.к. 
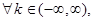 а интеграл
а интеграл 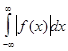 сходится, то согласно признаку Вейерштрасса (см. §1, гл.2), интеграл (1) сходится равномерно, а согласно теореме 2 §1, гл.2 функция
сходится, то согласно признаку Вейерштрасса (см. §1, гл.2), интеграл (1) сходится равномерно, а согласно теореме 2 §1, гл.2 функция 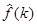 непрерывна. Вторую часть теоремы примем без доказательства.
непрерывна. Вторую часть теоремы примем без доказательства.
Теорема 2. Если 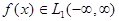 кусочно-непрерывная и имеет в каждой точке односторонние производные
кусочно-непрерывная и имеет в каждой точке односторонние производные 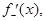
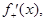 то в точках непрерывности функции
то в точках непрерывности функции 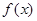 имеет место равенство
имеет место равенство
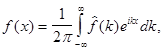 (2)
(2)
а в точках разрыва правая часть (2) равна полусумме пределов 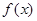 слева и справа (без доказательства).
слева и справа (без доказательства).
Замечание. Интеграл (2) сходится в смысле главного значения по Коши.
Равенства (1) и (2) называют соответственно прямым и обратным преобразованиями Фурье. Пишут 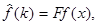
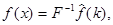
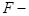 оператор Фурье.
оператор Фурье.
Преобразование Фурье аналогично преобразованию Лапласа и обладает аналогичными свойствами. В частности, согласно теореме 2 §1, гл.2.
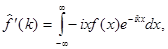 т.е. если
т.е. если 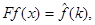 то
то 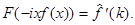 Это свойство аналогично свойству дифференцирования изображения по Лапласу. Можно доказать, что если
Это свойство аналогично свойству дифференцирования изображения по Лапласу. Можно доказать, что если 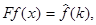 то
то 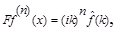 если
если 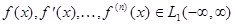 и
и 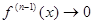 при
при 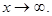
Если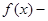 функция четная, то
функция четная, то
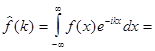
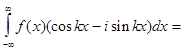
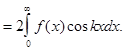 (3)
(3)
Из (3) видно, что 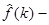 функция четная. Тогда
функция четная. Тогда 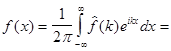
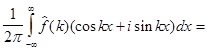
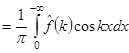 (4)
(4)
Итак, если 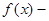 четная, то получаем косинус преобразования Фурье (3,4).
четная, то получаем косинус преобразования Фурье (3,4).
Аналогично, если 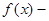 функция нечетная, получим синус-преобразование Фурье
функция нечетная, получим синус-преобразование Фурье
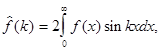 (5)
(5)
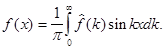 (6)
(6)
Подставим (1) в (2), получим
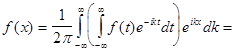
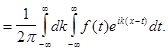 (7)
(7)
Формула (7) называется интегралом Фурье функции 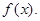 Ее можно записать в действительной форме
Ее можно записать в действительной форме
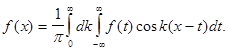 (8)
(8)
Сравним прямое и обратное преобразования Фурье (1,2) с рядом Фурье в комплексной форме:
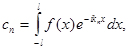 (9)
(9)
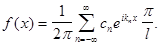 (10)
(10)
(Ради удобства множитель 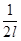 поставлен в формулу ряда Фурье, а не в формулу коэффициентов ряда Фурье). Частоты
поставлен в формулу ряда Фурье, а не в формулу коэффициентов ряда Фурье). Частоты 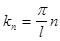 периодической функции
периодической функции 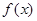 образуют арифметическую прогрессию
образуют арифметическую прогрессию 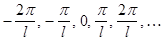 с разностью
с разностью 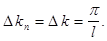 При неограниченном увеличении
При неограниченном увеличении 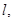 т.е. при
т.е. при 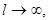
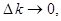 дискретный спектр становится непрерывным, а функция
дискретный спектр становится непрерывным, а функция 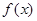 не периодической. При
не периодической. При 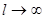 из (9) получим (1), а из (10) получим (2), т.е. вместо суммирования по дискретным частотам перейдем к интегрированию по параметру
из (9) получим (1), а из (10) получим (2), т.е. вместо суммирования по дискретным частотам перейдем к интегрированию по параметру 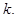 Поэтому функцию
Поэтому функцию 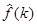 называют спектральной функцией (характеристикой), а
называют спектральной функцией (характеристикой), а 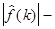 спектром функции
спектром функции 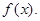 Этот спектр, согласно теореме 1, непрерывный.
Этот спектр, согласно теореме 1, непрерывный.
Пример. Представить интегралом Фурье функцию
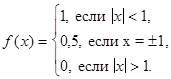
Решение. Найдем спектральную функцию
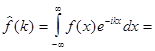
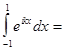
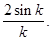 (11)
(11)
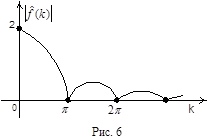
|
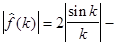 спектр данной функции
спектр данной функции
(см. рис. 6).
Подставляя (11) в (2), получим интеграл Фурье
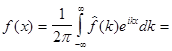
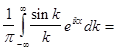
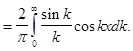 (12)
(12)
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 365; Нарушение авторских прав?; Мы поможем в написании вашей работы!