Многомерная случайная величина. Функция и плотность распределения

Рассмотрим случайную величину – точку разрыва снаряда на плоскости. Поскольку точка на плоскости характеризуется двумя координатами, то мы имеем дело уже не с одной, а с системой двух случайных величин (ξ, η). Аналогично, точка разрыва дистанционного снаряда в воздухе – система трех случайных величин (ξ, η, ζ). Это примеры многомерных случайных величин. Геометрически такие величины интерпретируются как случайные точки в n-мерном пространстве или как случайный вектор ξ=(ξ₁,ξ₂,…,ξ_n) этого пространства. Уточним понятие многомерной случайной величины. Пусть (Ω, 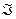, Р) – вероятностное пространство и пусть на Ω задано n случайных величин ξ₁,ξ₂,…, ξ_n. Совокупность (система) этих величин ξ=(ξ₁,ξ₂,…,ξ_n) и называется многомерной случайной величиной, или n-мерным случайным вектором, или случайной точкой n-мерного пространства. Сами величины ξ_i называются компонентами(координатами) вектора ξ.

Определение 1. Функция F(x₁,x₂,…,x_n) называется функцией распределения n-мерной случайной величины

ξ=(ξ₁,ξ₂,…,ξ_n), если она определена равенством

F(x₁,x₂,…,x_n)=P(ξ₁<x₁,ξ₂<x₂,…,ξ_n<x_n). (1)

Заметим, что событие

{ξ₁<x₁,ξ₂<x₂,…,ξ_n<x_n}=,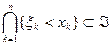

а поэтому вероятность в правой части (1) существует, и функция распределения определена в любой точке пространства R_n.

Если все компоненты случайного вектора являются дискретными, то и сам вектор называется дискретным.

Определение 2. Если существует неотрицательная функция f(x₁,x₂,…,x_n) такая, что при любых x₁,x₂,…,x_n выполняется равенство

, (2)

то случайный вектор ξ=(ξ₁,ξ₂,…,ξ_n) называется непрерывным. Функция f(x₁,x₂,…,x_n) называется плотностью распределения случайного вектора ξ.

Функция F(x₁,x₂,…,x_n) имеет смысл как для дискретного, так и для непрерывного случайного вектора. Плотность распределения f(x₁,x₂,…,x_n) имеет смысл только для непрерывной случайной величины, если иметь в виду обычные функции. Используя δ-функцию, можно и для дискретной случайной величины ввести понятие плотности. Остановимся подробнее на двумерной случайной величине (ξ, η) с функцией распределения F(x,y)=Р(ξ<x, η<y). Геометрически функция распределения F(x,y) означает вероятность попадания случайной точки в бесконечный квадрант с вершиной в точке (x, y), лежащий левее и ниже ее (см. заштрихованную часть на рисунке 17).

Функция распределения F₁(x) компоненты ξ вектора (ξ, η)

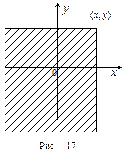
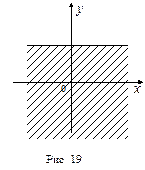
означает вероятность попасть в левую полуплоскость, ограниченную справа линией, параллельной оси Оy и проходящей через точку х (см. рис. 18). Функция распределения F₂(y) компоненты η вектора (ξ, η) означает вероятность попасть в нижнюю полуплоскость (см. рис. 19).

Из геометрической интерпретации легко понять свойства функции распределения F(x,y).

1) F(x,y) неубывающая функция;

2) F(-∞,y)= F(x,- ∞)= F (-∞,∞)=0;

3) F(x,+ ∞)= F₁(x), F(+∞,y)= F₂(y);

4) F(+∞,+∞)= 1.

Перепишем (2) для двумерной случайной величины

. (2¢)

Из (2¢) получим

,

. (3)

Дифференцируя (3) по переменным верхним пределам, найдем, что в точках непрерывности функции 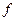(x,y)

,

. (4)

Таким образом, зная закон распределения двумерной случайной величины, мы всегда найдем закон распределения составляющих величин ξ и η. Аналогично, дифференцируя (2¢) по х и по y, получим

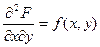. (5)

Из (2¢) ясно, что величину f(x,y)dxdy=f(x,y)ds можно интерпретировать как элементарную вероятность, т.е. вероятность попадания случайной точки (ξ,η) в элементарную площадку ds: Р((ξ,η)Îds)=f(x,y)ds. Поэтому вероятность попадания случайной точки в некоторую конечную область D можно определить так:

. (6)

Заметим, что все полученные формулы можно обобщить на n-мерную случайную величину. В частности

. (5¢)

Если дискретная случайная величина имеет конечное число возможных значений, то ее удобнее задавать в виде таблицы, где указаны все ее возможные значения и соответствующие вероятности. Для примера приведем такую таблицу для двумерной случайной величины (ξ,η)

h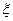
x1	x2	…	xn
y1	p11	p21	…	pn1	p(y1)
y2	p12	p22	…	pn2	p(y2)
			…
ym	p1m	p2m	…	pnm	p(ym)
	p(x1)	p(x2)	…	p(xn)

Здесь случайная величина ξ принимает n возможных значений, а случайная величина η – m возможных значений. .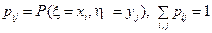

Первая и последняя строка таблицы дают ряд распределения случайной величины ξ, а первый и последний столбцы таблицы дают ряд распределения случайной величины η. При этом

,

. (7)

Пример 1. Дискретная случайная величина (ξ,η) задана таблицей. Найти ряд распределения для компонент ξ и η.

h	ξ	P(η=yi)
x1=1	x2=3	x3=4	x4=8
y1=3	0,15	0,06	0,25	0,04	0,5
y2=6	0,30	0,10	0,03	0,07	0,5
P(ξ=xi)	0,45	0,16	0,28	0,11

Решение. Суммируя, согласно (7), p_ij, стоящие в столбцах, получим ряд распределения случайной величины ξ (см. последнюю строку таблицы). Суммируя p_ij, стоящие в строках, получим ряд распределения случайной величины η (см. последний столбец таблицы).

Пример 2. Непрерывная случайная величина (ξ,η) задается плотностью распределения

.

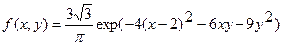Найти плотности компонент ξ и η f₁(x) и f₂(y).

Решение. Воспользуемся формулами (4).

.

=.

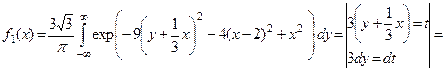
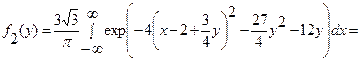
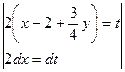
Дата добавления: 2014-01-07