Алгоритм кируса-бека

Задача: убрать невидимую часть отрезка

Условие работы алгоритма: отсекаемый многоугольник должен быть выпуклым.

Окно – видимая область, в которой все происходит.

Для вычисления координат точек относительно окна используются нормали.

j

b F

R

a Θ n_i

i

n(b-a)≥0

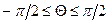; CosΘ≥0;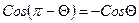

Для работы с этим алгоритмом будем пользоваться параметрическим представлением прямой (отрезка).

p(t)=p1+(p2-p1)t, 0≤t≤1

Точка F – некоторая граничная точка области, расположенная на пересечении двух границ этой области.

Все возможные направления вектора p(t)-F:

1. n(p(t)-F)<0 – вектор направлен во вне области F
2. n(p(t)-F)=0 – вектор принадлежит плоскости, проходящей через точку F и перпендикулярный плоскости
3. n(p(t)-F)>0 – вектор направлен во внутрь области F

бесконечная прямая будет пересекать выпуклую область F ровно в двух точках

Если F лежит на нормали плоскости, то p(t) будет являться пересечением плоскости с прямой.

Пример 1: Частично видимый отрезок

4

p2(9;3)

n_л n_в n_п

p1(-1;1) n_н

8

p(t) = [-1;1]+[10;2]t = (10t-1)i+(2t+1)j

а. Выбираем точку F(0;0)

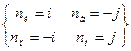- нормали (лево, право, верх, низ)

n_л = [-1;1]+[10;2]x1/10 = [0;1,2]

б. F(8;4) t=9/10

p(9/10) = [8;2.8]

Если мы используем F(0;0) для нижней грани, то n_н(p(t)-F)=0; 2t+1=0; t=-1/2 – что неверно, т.к. 0≤t≤1

На самом деле: при работе с алгоритмом Кируса-Бека очень важно знать ориентацию отрезка.

Пример 2: Нетривиальный невидимый отрезок

p6(10;1)

8

p5(6;-2)

p(t) = [6;-2]+[4;3]t

левый: t=-3/2 – сразу отсекаем, т.к. 0≤t≤1

верхний: t=2 – сразу отсекаем, т.к. 0≤t≤1

правый: t=1/2 и нижний: t=2/3 также не являются точками пересечения (при учете ориентации)

Дата добавления: 2014-01-07