Исследование нелинейных систем

Типовая структурная схема нелинейных систем.

Наиболее распространенная структурная схема нелинейной системы имеет вид:

Рис. 4.24.

где НЭ - нелинейный элемент;

ЛЧ – линейная часть

Рассмотрим уравнения этой системы, связывающее входной (r) и выходной (y) сигналы.

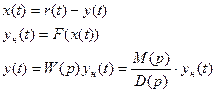(4.8)

Уравнение, связывающее входной и выходной сигнал нелинейного элемента (x и y_Н) имеет вид:

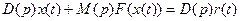(4.9)

ПРИМЕР

Пусть дана следующая нелинейная система:

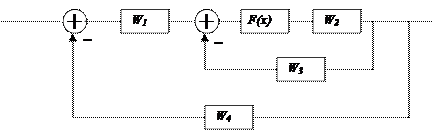Рис. 4.25.

Необходимо ее преобразовать к типовому виду (Рис. 4.24). Для этого осуществляется перенос первого сумматора на выход звена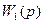

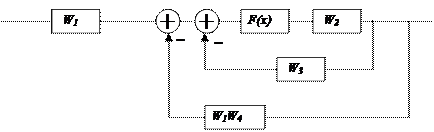Рис. 4.26.

Затем объединяются две ветви обратной связи

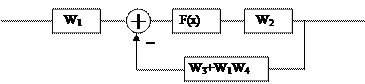Рис. 4.27.

Далее система приводится к единичной обратной связи

Рис. 4.28.

Полученная нелинейная система отличается от типовой двумя дополнительными линейными звеньями: на входе и выходе системы. Линейное звено 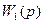можно исключить из системы, заменив входной сигнал по формуле:

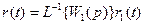(4.10)

А зная сигнал 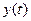, можно получить выходной сигнал системы по выражению:

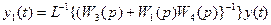(4.11)

Таким образом, для анализа свойств нелинейной системы можно ограничиться рассмотрением типовой схемы нелинейной системы (Рис. 4.24).

ПРИМЕР

Вывести уравнение, связывающее входной и выходной сигнал нелинейного элемента (x и y_Н)

Рис. 4.29.

Где 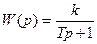, а нелинейный элемент – реле, имеющий статическую характеристику :

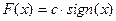Рис. 4.30.

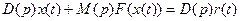(4.12)

(4.13)

Если входной сигнал – единичное ступенчатое воздействие, то (4.13) принимает вид

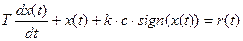(4.14)

При анализе нелинейных систем обычно решают следующие задачи:

· Решение задачи устойчивости нелинейных систем, которая сводится к определению: устойчивости в целом (или абсолютной устойчивости); устойчивости в малом и устойчивости в большом.

· Определение возможности возникновения автоколебания: определение параметров системы, при которых они возникают; определение параметров автоколебаний (амплитуды, частоты).

Как отмечалось выше, что режим автоколебаний является наиболее неблагоприятным, поэтому задача определения возможности автоколебаний в нелинейных системах является первоочередной.

Дата добавления: 2014-01-07