Величина

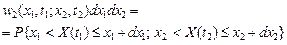(2.8)

являє собою ймовірність того, що X(t) знаходиться у момент часу t = t₁ в інтервалі від х ₁ до х ₁ + dx₁, а у момент часу t = t₂ - в інтервалі від х ₂ до х ₂ + dx₂.

Двомірною щільністю ймовірності (2.7) повністю характеризуються так звані марковські випадкові процеси (за ім’ям відомого математика, академіка Петербурзької АН Андрія Андрійовича Маркова, який уперше дослідив ці процеси), для яких знання значення процесу у момент часу t_k містить усю можливу інформацію про подальший хід процесу.

Аналогічно можна увести поняття про n -мірну функцію розподілу і n -мірну щільність ймовірності. Чим вище порядок n, тим повніше описуються статистичні властивості випадкового процесу, але багатомірні закони розподілу є громіздкими і незручними для використання. Тому частіше обмежуються випадками, коли для опису випадкового процесу достатньо знати тільки одномірний чи двомірний закон розподілу.

У практиці досліджень систем автоматичного управління широке розповсюдження отримали порівняно більш прості, хоча й менш повні характеристики випадкових процесів, аналогічні числовим характеристикам випадкових величин: математичне сподівання, дисперсія, середнє значення квадрата випадкового процесу, кореляційна функція, спектральна щільність та інші.

Математичним сподіванням (середнім значенням) m_x(t) випадкового процесу X(t) називають величину:

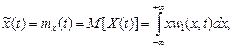(2.9)

де w₁(x, t) – одномірна щільність ймовірності випадкового процесу X(t).

Математичне сподівання випадкового процесу X(t) являє собою деяку невипадкову (регулярну) функцію часу m_x(t), біля якої групуються і відносно якої коливаються усі реалізації даного випадкового процесу. Математичне сподівання називають середнім значенням випадкового процесу за множиною (статистичним середнім), оскільки воно являє собою ймовірносно усереднене значення нескінченної множини реалізацій випадкового процесу.

Середнім значенням квадрата випадкового процесу називають величину:

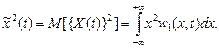(2.10)

Часто розглядають так званий центрований випадковий процес 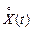- відхилення випадкового процесу X(t) від його середнього значення m_x(t):

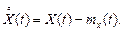(2.11)

Тоді випадковий процес X(t) можна розглядати як суму двох складових: регулярної складової, що дорівнює математичному сподіванню m_x(t), і центрованої випадкової складової 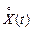, тобто:

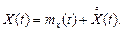(2.12)

Зрозуміло, що математичне сподівання центрованого випадкового процесу дорівнює нулю:

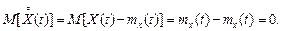(2.13)

Для того, щоб урахувати ступінь розкидання реалізацій випадкового процесу відносно його середнього значення, застосовують поняття дисперсії випадкового процесу, яка дорівнює математичному сподіванню квадрата центрованого випадкового процесу:

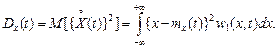(2.14)

Дисперсія випадкового процесу є невипадковою (регулярною) функцією D_x(t), значення якої у кожен момент часу t_k дорівнює дисперсії відповідного перерізу X(t_k) випадкового процесу.

Математичне сподівання m_x(t), дисперсія D_x(t) і середнє значення квадрата 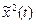випадкового процесу зв’язані співвідношенням:

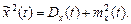(2.15)

Із (2.15) видно, що середнє значення квадрата випадкового процесу 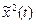у деякій мірі ураховує і середнє значення випадкового процесу, і ступінь розкидання його реалізацій відносно цього середнього значення, тому воно широко використовується як оцінка точності систем автоматичного управління.

Іноді зручно використовувати статистичні характеристики випадкового процесу, які мають ту саму розмірність, що й сама випадкова величина:

- середнє квадратичне значення випадкового процесу:

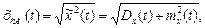(2.16)

що дорівнює арифметичному значенню квадратного кореня із середнього значення квадрата випадкового процесу;

- середнє квадратичне відхилення випадкового процесу:

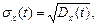(2.17)

що дорівнює арифметичному значенню квадратного кореня із дисперсії випадкового процесу.

Характеристику (2.17) використовують тільки для центрованих випадкових процесів.

Знання указаних вище статистичних характеристик часто є достатнім для вирішення багатьох задач теорії автоматичного керування.

Дата добавления: 2014-01-07