Корекція імпульсних систем

Загальна мета корекції імпульсних систем полягає у забезпеченні стійкості, заданої точності роботи в усталеному режимі, задовільної якості перехідних процесів.

Корекцію можна здійснювати за рахунок зміни параметрів системи без зміни її структури або за рахунок введення додаткових корегуючих кіл. Причому для корекції імпульсних систем є більш широкі можливості, оскільки коректуючі пристрої можуть бути безперервними або дискретними.

Найпростішим способом корекції є зміна коефіцієнта підсилення К розімкнутої системи, який впливає практично на всі властивості системи. При цьому необхідно пам’ятати, що коефіцієнт К не повинен перевищувати критичного значення, при якому система знаходиться на межі стійкості.

Приклад 3.11 Визначити, при яких значеннях коефіцієнта К імпульсна система стійка у замкнутому стані, якщо передавальна функція розімкнутої системи має вигляд:

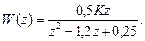
Запишемо характеристичне рівняння замкнутої системи:

D(z) = z² – 1,2z + 0,25 + 0,5Kz = z² + z(0,5K - 1,2) + 0,25 = 0.

Після w-перетворення отримуємо характеристичне рівняння:

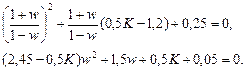
Для стійкості системи другого порядку необхідно і достатньо, щоб усі коефіцієнти цього характеристичного рівняння були додатними. При додатних значеннях коефіцієнта К дана система буде стійкою, якщо виконується умова:

2,45 – 0,5К > 0, тобто К < 4,9.

Отже, імпульсна система стійка при К < 4,9.

Корекція імпульсної системи за рахунок введення корегуючих пристроїв полягає у зміні частотних характеристик системи з метою максимального їх наближення до бажаних.

Як і у безперервних системах, безперервний корегуючий пристрій можна вводити послідовно з ланками незмінюваної частини системи, паралельно деяким з них, а також у вигляді зворотного зв’язку, що охоплює всю систему або частину її ланок.

Визначення параметрів послідовного корегуючого пристрою є досить складною задачею. У найпростішому випадку при досить високій частоті квантування і великій інерційності безперервної частини, коли виконується умова (3.35) теореми Котельникова-Шеннона, імпульсну систему можна замінити безперервною і тоді записати:

(3.64)

де - частотні характеристики: бажана, корегуючого пристрою, безперервної частини початкової системи; k_i – коефіцієнт передачі імпульсного елемента.

З урахуванням тривалості імпульсів (g¹0) вираз (3.64) матиме вигляд:

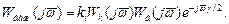(3.65)

Після заміни імпульсної системи безперервною синтез послідовного корегуючого пристрою можна виконати методами, що розроблені для безперервних систем, зокрема методом логарифмічних частотних характеристик.

Дата добавления: 2014-01-07